El método de Romberg
aplicando la extrapolación de Richardson ( Richardson 1911 ) repetidamente sobre la regla del trapecio o la regla del rectángulo (regla del punto medio). Las estimaciones generan una matriz triangular . El método de Romberg es una fórmula de Newton-Cotes : evalúa el integrando en puntos igualmente espaciados. El integrando debe tener derivadas continuas, aunque se pueden obtener resultados bastante buenos si solo existen unas pocas derivadas. Si es posible evaluar el integrando en puntos desigualmente espaciados, entonces otros métodos como la cuadratura de Gauss y la cuadratura de Clenshaw-Curtis son generalmente más precisos.
donde y . En notación O grande , el error para R ( n , m ) es ( Mysovskikh 2002 ) :
La extrapolación cero, R ( n , 0), es equivalente a la regla trapezoidal con 2 n + 1 puntos; la primera extrapolación, R ( n , 1), es equivalente a la regla de Simpson con 2 n + 1 puntos. La segunda extrapolación, R ( n , 2), es equivalente a la regla de Boole con 2 n + 1 puntos. Otras extrapolaciones difieren de las fórmulas de Newton-Cotes. En particular, otras extrapolaciones de Romberg amplían la regla de Boole de manera muy leve, modificando los pesos en proporciones similares a las de la regla de Boole. Por el contrario, otros métodos de Newton-Cotes producen pesos cada vez más diferentes, lo que eventualmente conduce a grandes pesos positivos y negativos. Esto es indicativo de cómo los métodos polinomiales de Newton-Cotes de interpolación de gran grado no logran converger para muchas integrales, mientras que la integración de Romberg es más estable.
Cuando las evaluaciones de funciones son costosas, puede ser preferible reemplazar la interpolación polinómica de Richardson con la interpolación racional propuesta por Bulirsch y Stoer (1967) .
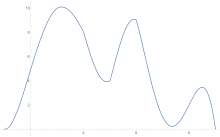
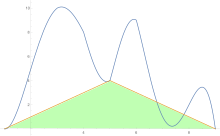
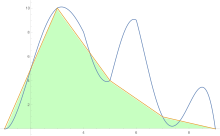
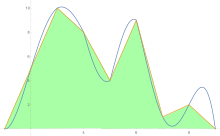
Para estimar el área bajo una curva, la regla del trapecio se aplica primero a una pieza, luego a dos, luego a cuatro, y así sucesivamente.
Como ejemplo, la función gaussiana está integrada de 0 a 1, es decir, la función de error erf (1) ≈ 0.842700792949715. La matriz triangular se calcula fila por fila y el cálculo finaliza si las dos últimas entradas en la última fila difieren menos de 10 −8 .