Línea Simson

La línea de Simson LN (roja) del triángulo ABC con respecto al punto P en el círculo circunferencial

En geometría , dado un triángulo ABC y un punto P en su circunferencia , los tres puntos más cercanos a P en las líneas AB , AC y BC son colineales . ^[1] La línea que pasa por estos puntos es la línea de Simson de P , llamada así por Robert Simson . ^[2] Sin embargo, el concepto fue publicado por primera vez por William Wallace en 1799. ^[3]

Lo contrario también es cierto; si los tres puntos más cercanos a P en tres líneas son colineales y no hay dos líneas paralelas, entonces P se encuentra en el círculo circunferencial del triángulo formado por las tres líneas. O en otras palabras, la línea de Simson de un triángulo ABC y un punto P es solo el triángulo pedal de ABC y P que se ha degenerado en una línea recta y esta condición obliga al lugar geométrico de P a trazar el círculo circunferencial del triángulo ABC .

Ecuación

Colocando el triángulo en el plano complejo, deje que el triángulo ABC con circunferencia unitaria tenga vértices cuyas ubicaciones tengan coordenadas complejas a , b , c , y sea P con coordenadas complejas p un punto en la circunferencia circunferencial. La recta de Simson es el conjunto de puntos z que satisface ^{[4] : Proposición 4}

${\displaystyle 2abc{\bar {z}}-2pz+p^{2}+(a+b+c)p-(bc+ca+ab)-{\frac {abc}{p}}=0,}$

donde una barra superior indica una conjugación compleja .

Propiedades

Las líneas de Simson (en rojo) son tangentes al deltoides de Steiner (en azul).

• La línea de Simson de un vértice del triángulo es la altura del triángulo que cae desde ese vértice, y la línea de Simson del punto diametralmente opuesto al vértice es el lado del triángulo opuesto a ese vértice.
• Si P y Q son puntos en el círculo circunferencial, entonces el ángulo entre las líneas de Simson de P y Q es la mitad del ángulo del arco PQ . En particular, si los puntos son diametralmente opuestos, sus líneas de Simson son perpendiculares y, en este caso, la intersección de las líneas se encuentra en el círculo de nueve puntos.
• Si H denota el ortocentro del triángulo ABC , la línea de Simson de P biseca el segmento PH en un punto que se encuentra en el círculo de nueve puntos.
• Dados dos triángulos con la misma circunferencia circunscrita, el ángulo entre las líneas de Simson de un punto P en la circunferencia circunscrita por ambos triángulos no depende de P .
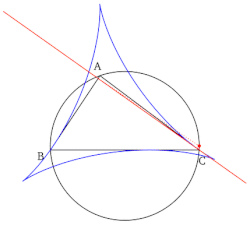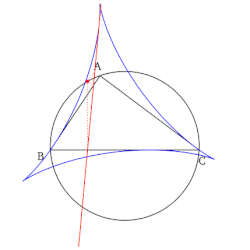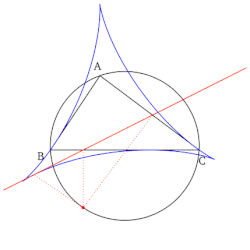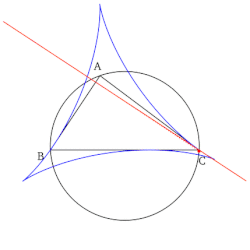
• El conjunto de todas las líneas de Simson, cuando se dibujan, forman un sobre en forma de deltoides conocido como deltoides de Steiner del triángulo de referencia.
• La construcción de la línea de Simson que coincide con un lado del triángulo de referencia (ver la primera propiedad arriba) produce un punto no trivial en esta línea lateral. Este punto es el reflejo del pie de la altitud (que cae sobre la línea lateral) sobre el punto medio de la línea lateral que se está construyendo. Además, este punto es un punto tangente entre el lado del triángulo de referencia y su deltoides de Steiner.
• Un cuadrilátero que no es un paralelogramo tiene un solo punto del pedal, llamado punto de Simson, con respecto al cual los pies del cuadrilátero son colineales. ^[5] El punto de Simson de un trapezoide es el punto de intersección de los dos lados no paralelos. ^{[6] : pág. 186}
• Ningún polígono convexo con al menos 5 lados tiene una línea de Simson. ^[7]

Prueba de existencia

El método de prueba es demostrar eso . es un cuadrilátero cíclico, entonces . es un cuadrilátero cíclico ( teorema de Thales ), entonces . De ahí . Ahora es cíclico, entonces . Por lo tanto .${\displaystyle \angle NMP+\angle PML=180^{\circ }}$${\displaystyle PCAB}$${\displaystyle \angle PBA+\angle ACP=\angle PBN+\angle ACP=180^{\circ }}$${\displaystyle PMNB}$${\displaystyle \angle PBN+\angle NMP=180^{\circ }}$${\displaystyle \angle NMP=\angle ACP}$${\displaystyle PLCM}$${\displaystyle \angle PML=\angle PCL=180^{\circ }-\angle ACP}$${\displaystyle \angle NMP+\angle PML=\angle ACP+(180^{\circ }-\angle ACP)=180^{\circ }}$

la línea verde es la línea de Simson, las azules son las perpendiculares caídas.

Cualquiera que sea el punto Z en la figura adyacente, a + c es 90. Además, cualquiera que sea el punto Z, cyb serán iguales. Por lo tanto, tenemos lo siguiente:

a + c = 90

∴ a + b = 90… (c y b son iguales) (1)

Ahora, considere la medida del ángulo: a + 90 + b.

Si mostramos que este ángulo es 180, entonces se demuestra el teorema de Simson.

De (1) tenemos, a + 90 + b = 180

QED

Generalizaciones

Generalización 1

Las proyecciones de Ap, Bp, Cp sobre BC, CA, AB son tres puntos colineales

• Sea ABC un triángulo, deje que una línea ℓ pase por el circuncentro O , y deje que un punto P se encuentre en el círculo circunferencial. Deje que AP, BP, CP se encuentren ℓ en A _p , B _p , C _p respectivamente. Sean A ₀ , B ₀ , C ₀ las proyecciones de A _p , B _p , C _p sobre BC, CA, AB , respectivamente. Entonces A ₀ , B ₀ , C ₀son colineales. Además, la nueva línea pasa por el punto medio de PH , donde H es el ortocentro de Δ ABC . Si ℓ pasa por P , la línea coincide con la línea de Simson. ^{[8] [9] [10]}

Una versión proyectiva de una línea Simson

Generalización 2

• Deje que los vértices del triángulo ABC se encuentren en la cónica Γ, y sean Q, P dos puntos en el plano. Deje que PA, PB, PC se crucen con la cónica en A ₁ , B ₁ , C ₁ respectivamente. QA _{1 se} cruza con BC en A ₂ , QB _{1 se} cruza con AC en B ₂ y QC _{1 se} cruza con AB en C ₂ . Entonces los cuatro puntos A ₂ ,B ₂ , C ₂ y P son colineales si solo Q se encuentra en la cónica Γ. ^[11]

Generalización 3

• RF Cyster generalizó el teorema a cuadriláteros cíclicos en Las líneas de Simson de un cuadrilátero cíclico

Ver también

• Triángulo de pedales
• Robert Simson

Referencias

1. HSM Coxeter y SL Greitzer, Geometría revisada , Matemáticas. Assoc. América, 1967: p.41.
2. "Historia de Gibson 7 - Robert Simson" . 2008-01-30.
3. http://www-groups.dcs.st-and.ac.uk/history/Biographies/Wallace.html
4. Todor Zaharinov, "El triángulo de Simson y sus propiedades", Forum Geometricorum 17 (2017), 373-381. http://forumgeom.fau.edu/FG2017volume17/FG201736.pdf
5. Daniela Ferrarello, Maria Flavia Mammana y Mario Pennisi, "Pedal Polygons", Forum Geometricorum 13 (2013) 153-164: Teorema 4.
6. Olga Radko y Emmanuel Tsukerman, "La construcción de la bisectriz perpendicular, el punto isóptico y la línea de Simson de un cuadrilátero", Forum Geometricorum 12 (2012). [1]
7. Tsukerman, Emmanuel (2013). "Sobre polígonos que admiten una línea de Simson como análogos discretos de parábolas" (PDF) . Foro Geometricorum . 13 : 197-208.
8. "Una generalización de la línea Simson" . Corta el nudo. Abril de 2015.
9. Nguyen Van Linh (2016), "Otra prueba sintética de la generalización de Dao del teorema de la línea de Simson" (PDF) , Forum Geometricorum , 16 : 57-61
10. Nguyen Le Phuoc y Nguyen Chuong Chi (2016). 100.24 Una prueba sintética de la generalización de Dao del teorema de la línea de Simson. The Mathematical Gazette, 100, págs. 341-345. doi: 10.1017 / mag.2016.77. La Gaceta Matemática
11. Smith, Geoff (2015), "99.20 Una línea proyectiva de Simson" , The Mathematical Gazette , 99 (545): 339–341, doi : 10.1017 / mag.2015.47

enlaces externos

Wikimedia Commons tiene medios relacionados con la línea Simson .

• Simson Line en cut-the-knot .org
• FM Jackson y Weisstein, Eric W. "Simson Line" . MathWorld .
• Una generalización del teorema de Neuberg y la línea de Simson-Wallace en Dynamic Geometry Sketches , un boceto interactivo de geometría dinámica.