Racional diádico

Fracción con una potencia de dos como denominador

Racionales diádicos en el intervalo de 0 a 1.

En matemáticas, un racional diádico o racional binario es un número que se puede expresar como una fracción cuyo denominador es una potencia de dos . Por ejemplo, 1/2, 3/2 y 3/8 son racionales diádicos, pero 1/3 no lo es. Estos números son importantes en informática porque son los únicos con representaciones binarias finitas . Los racionales diádicos también tienen aplicaciones en pesos y medidas, firmas de compás musicales y educación matemática temprana. Pueden aproximarse con precisión a cualquier número real .

La suma, diferencia o producto de dos números racionales diádicos cualesquiera es otro número racional diádico, dado por una fórmula simple. Sin embargo, la división de un número racional diádico por otro no siempre produce un resultado racional diádico. Matemáticamente, esto significa que los números racionales diádicos forman un anillo , que se encuentra entre el anillo de los números enteros y el campo de los números racionales . Este anillo se puede denotar${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]}$.

En matemáticas avanzadas, los números racionales diádicas son fundamentales para las construcciones de la electroválvula diádico , la función de signo de interrogación de Minkowski , Daubechies ondas , grupo de Thompson , Prüfer-2 grupos , números surreales , y los números de fusibles . Estos números son orden-isomorfos a los números racionales; forman un subsistema de números 2-ádicos así como de los reales, y pueden representar las partes fraccionarias de números 2-ádicos. Se han utilizado funciones desde números naturales hasta racionales diádicos para formalizar el análisis matemático enmatemáticas inversas .

Aplicaciones

En medida

Muchos sistemas tradicionales de pesos y medidas se basan en la idea de dividir a la mitad repetidamente, lo que produce racionales diádicos al medir cantidades fraccionarias de unidades. La pulgada se subdivide habitualmente en racionales diádicos en lugar de utilizar una subdivisión decimal. ^[1] Las divisiones habituales del galón en medio galón, cuartos de galón , pintas y tazas también son diádicas. ^[2] Los antiguos egipcios usaban racionales diádicos en la medición, con denominadores de hasta 64. ^[3] De manera similar, los sistemas de pesos de la civilización del valle del Indose basan en su mayor parte en reducciones a la mitad repetidas; antropóloga Heather M.-L. Miller escribe que "la reducción a la mitad es una operación relativamente simple con balances de vigas, que es probablemente la razón por la que tantos sistemas de peso de este período de tiempo usaban sistemas binarios". ^[4]

En informática

Los racionales diádicos son fundamentales para la informática como un tipo de número fraccionario que muchas computadoras pueden manipular directamente. En particular, como tipo de datos utilizado por las computadoras, los números de punto flotante a menudo se definen como números enteros multiplicados por potencias positivas o negativas de dos. Los números que se pueden representar con precisión en un formato de punto flotante, como los tipos de datos de punto flotante IEEE , se denominan números representables. Para la mayoría de las representaciones de punto flotante, los números representables son un subconjunto de los racionales diádicos. ^[5] Lo mismo ocurre con los tipos de datos de coma fija , que también utilizan poderes de dos implícitamente en la mayoría de los casos. ^[6]Debido a la simplicidad de la computación con racionales diádicos, también se usan para computación real exacta usando aritmética de intervalos , ^[7] y son fundamentales para algunos modelos teóricos de números computables . ^{[8] [9] [10]}

La generación de una variable aleatoria a partir de bits aleatorios, en un período de tiempo fijo, solo es posible cuando la variable tiene un número finito de resultados cuyas probabilidades son todos números racionales diádicos. Para las variables aleatorias cuyas probabilidades no son diádicas, es necesario aproximar sus probabilidades mediante racionales diádicas o utilizar un proceso de generación aleatoria cuyo tiempo sea en sí mismo aleatorio e ilimitado. ^[11]

En música

Cinco barras de Igor Stravinski 's La consagración de la primavera
mostrando los compases${\displaystyle {\tfrac {3}{16}}}$, ${\displaystyle {\tfrac {2}{16}}}$, ${\displaystyle {\tfrac {3}{16}}}$, y ${\displaystyle {\tfrac {2}{8}}}$

Las firmas de tiempo en la notación musical occidental se escriben tradicionalmente en una forma que se asemeja a las fracciones (por ejemplo:${\displaystyle {\tfrac {2}{2}}}$, ${\displaystyle {\tfrac {4}{4}}}$, o ${\displaystyle {\tfrac {6}{8}}}$), ^[12] aunque la línea horizontal del pentagrama musical que separa el número superior e inferior a menudo se omite cuando se escribe la firma por separado de su pentagrama. Como fracciones, generalmente son diádicas, ^[13] aunque también se han utilizado firmas de tiempo no diádicas . ^[14] El valor numérico de la firma, interpretado como una fracción, describe la longitud de un compás como una fracción de una nota entera . Su numerador describe el número de tiempos por compás y el denominador describe la duración de cada tiempo. ^{[12] [13]}

En educación matemática

En las teorías del desarrollo infantil del concepto de fracción basadas en el trabajo de Jean Piaget , los números fraccionarios que surgen de la reducción a la mitad y la reducción repetida a la mitad se encuentran entre las primeras formas de fracciones en desarrollarse. ^[15] Esta etapa de desarrollo del concepto de fracciones se ha denominado "reducción a la mitad algorítmica". ^[16] La suma y resta de estos números se puede realizar en pasos que solo implican doblar, dividir por la mitad, sumar y restar números enteros. Por el contrario, la suma y resta de fracciones más generales implica la multiplicación y factorización de números enteros para alcanzar un denominador común. Por lo tanto, las fracciones diádicas pueden ser más fáciles de calcular para los estudiantes que las fracciones más generales. ^[17]

Aritmética

La suma , el producto o la diferencia de dos racionales diádicos cualesquiera es en sí mismo otro racional diádico, y puede calcularse mediante las siguientes fórmulas: ^[18]

$${\displaystyle {\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}={\frac {2^{d-\min(b,d)}a+2^{b-\min(b,d)}c}{2^{\max(b,d)}}}}$$

$${\displaystyle {\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}={\frac {2^{d-b}a-c}{2^{d}}}\quad (d\geq b)}$$

$${\displaystyle {\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}={\frac {a-2^{b-d}c}{2^{b}}}\quad (d<b)}$$

$${\displaystyle {\frac {a}{2^{b}}}\times {\frac {c}{2^{d}}}={\frac {a\times c}{2^{b+d}}}.}$$

Sin embargo, el resultado de dividir un racional diádico por otro no es necesariamente un racional diádico. ^[19]

Propiedades adicionales

Todo entero y todo medio entero es un racional diádico. ^[20]

Cada número real puede aproximarse de manera arbitraria y cercana mediante racionales diádicos. En particular, para un número real${\displaystyle x}$, los racionales diádicos de la forma ${\displaystyle \left\lfloor 2^{i}x\right\rfloor /2^{i}}$ aproximado ${\displaystyle x}$ de abajo a dentro de un error de ${\displaystyle 1/2^{i}}$, que puede hacerse arbitrariamente pequeño eligiendo ${\displaystyle i}$ser arbitrariamente grande. Para un subconjunto fractal de los números reales, este límite de error es óptimo: para estos números, no hay valor de${\displaystyle i}$ para el cual el error es menor que una constante veces ${\displaystyle 1/2^{i}}$. ^[21] La existencia de aproximaciones diádicas precisas se puede expresar diciendo que el conjunto de todos los racionales diádicos es un denso en la línea real . ^[20] Más fuertemente, este conjunto es uniformemente denso, en el sentido de que los racionales diádicos con denominador${\displaystyle 2^{i}}$están espaciados uniformemente en la línea real. ^[8]

Los racionales diádicos son precisamente aquellos números que poseen expansiones binarias finitas . ^[8] Sus expansiones binarias no son únicas; hay una representación finita y una infinita de cada racional diádico diferente de 0 (ignorando los ceros terminales). Por ejemplo, 0.1 ₂  = 0.0111 ... ₂  = 1/4 + 1/8 + 1/16 +… = 1/2. Además, 0.11 ₂  = 0.10111 ... ₂  = 3/4. ^{[8] [22]} Los racionales diádicos son los únicos números cuyas expansiones binarias no son únicas. ^[8]

En matemáticas avanzadas

Estructura algebraica

Debido a que están cerrados bajo suma, resta y multiplicación, pero no división, los racionales diádicos son un anillo pero no un campo . ^[23] El anillo de los racionales diádicos puede denotarse${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]}$, lo que significa que se puede generar evaluando polinomios con coeficientes enteros, en el argumento ${\displaystyle {\tfrac {1}{2}}}$. ^[24] Como anillo, los racionales diádicos son un subanillo de los números racionales y un subanillo de los enteros. ^[25] Algebraicamente, este anillo es la localización de los números enteros con respecto al conjunto de potencias de dos . ^[26]

Además de formar un subanillo de los números reales , los números racionales diádicos forman un subanillo de los números 2-ádicos , un sistema de números que se puede definir a partir de representaciones binarias que son finitas a la derecha del punto binario pero que pueden extenderse infinitamente. muy a la izquierda. Los números 2-ádicos incluyen todos los números racionales, no solo los racionales diádicos. Incrustar los racionales diádicos en los números 2-ádicos no cambia la aritmética de los racionales diádicos, pero les da una estructura topológica diferente a la que tienen como subanillo de los números reales. Como lo hacen en los reales, los racionales diádicos forman un subconjunto denso de los números 2-ádicos, ^[27]el conjunto de números 2-ádicos con expansiones binarias finitas. Cada número 2-ádico se puede descomponer en la suma de un número entero 2-ádico y un racional diádico; en este sentido, los racionales diádicos pueden representar las partes fraccionarias de números 2-ádicos, pero esta descomposición no es única. ^[28]

Adición de racionales diádicos módulo 1 (el grupo cociente ${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]/\mathbb {Z} }$de los racionales diádicos por los números enteros) forma el grupo 2 de Prüfer . ^[29]

Solenoide diádico

Considerar solo las operaciones de suma y resta de los racionales diádicos les da la estructura de un grupo abeliano aditivo . La dualidad de Pontryagin es un método para comprender los grupos abelianos mediante la construcción de grupos duales, cuyos elementos son caracteres del grupo original, homomorfismos de grupo al grupo multiplicativo de los números complejos , con la multiplicación puntual como la operación de grupo dual. El grupo dual de los racionales diádicos aditivos, así construido, también puede verse como un grupo topológico . Se llama solenoide diádico y es isomorfo al producto topológico de los números reales y los números 2-ádicos, coorientadospor la inserción diagonal de los racionales diádicos en este producto. ^[27] Es un ejemplo de un protorus , un solenoide y un continuo indecomponible . ^[30]

Funciones con racionales diádicos como puntos distinguidos

La función de signo de interrogación de Minkowski asigna números racionales a racionales diádicos

A Daubechies Wavelet , mostrando puntos de no-uniformidad en racionales diádicas

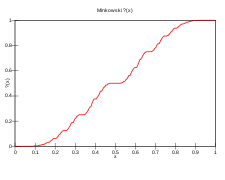
Debido a que son un subconjunto denso de los números reales, los racionales diádicos, con su orden numérico, forman un orden denso . Al igual que con dos órdenes lineales densos contables ilimitados, según el teorema del isomorfismo de Cantor , ^[31] los racionales diádicos son orden-isomorfos a los números racionales. En este caso, la función del signo de interrogación de Minkowski proporciona una biyección que preserva el orden entre el conjunto de todos los números racionales y el conjunto de los racionales diádicos. ^[32]

Los racionales diádicos juegan un papel clave en el análisis de las ondas de Daubechies , como el conjunto de puntos donde la función de escala de estas ondas no es uniforme. ^[23] De manera similar, los racionales diádicos parametrizan las discontinuidades en el límite entre puntos estables e inestables en el espacio de parámetros del mapa de Hénon . ^[33]

El conjunto de homeomorfismos lineales por partes desde el intervalo unitario hasta sí mismo que tienen pendientes de potencia de 2 y puntos de corte diádico-racionales forma un grupo bajo la operación de composición de funciones . Este es el grupo de Thompson , el primer ejemplo conocido de un grupo simple infinito pero presentado de manera finita . ^[34] El mismo grupo también puede ser representado por una acción sobre árboles binarios enraizados, ^[35] o por una acción sobre los racionales diádicos dentro del intervalo unitario. ^[29]

Otras construcciones relacionadas

En matemáticas inversas , una forma de construir los números reales es representarlos como funciones de números unarios a racionales diádicos, donde el valor de una de estas funciones para el argumento${\displaystyle i}$ es un racional diádico con denominador ${\displaystyle 2^{i}}$que se aproxima al número real dado. Definir números reales de esta manera permite probar muchos de los resultados básicos del análisis matemático dentro de una teoría restringida de aritmética de segundo orden llamada "análisis factible" (BTFA). ^[36]

Los números surrealistas se generan mediante un principio de construcción iterado que comienza generando todos los racionales diádicos finitos, y luego continúa creando nuevos y extraños tipos de infinitos, infinitesimales y otros números. ^[37] Este sistema numérico es fundamental para la teoría de juegos combinatorios , y los racionales diádicos surgen naturalmente en esta teoría como el conjunto de valores de ciertos juegos combinatorios. ^{[38] [39] [40]}

Los números fusibles son un subconjunto de los racionales diádicos, el cierre del conjunto${\displaystyle \{0\}}$ bajo la operación ${\displaystyle x,y\mapsto (x+y+1)/2}$, restringido a parejas ${\displaystyle x,y}$ con ${\displaystyle |x-y|<1}$. Están bien ordenados , con un tipo de orden igual al número épsilon ${\displaystyle \varepsilon _{0}}$. Por cada entero${\displaystyle n}$ el número de fusible más pequeño que es mayor que ${\displaystyle n}$ tiene la forma ${\displaystyle n+1/2^{k}}$. La existencia de${\displaystyle k}$ para cada ${\displaystyle n}$no se puede probar en la aritmética de Peano , ^[41] y${\displaystyle k}$ crece tan rápidamente en función de ${\displaystyle n}$ Eso para ${\displaystyle n=3}$es (en la notación de flecha hacia arriba de Knuth para números grandes) ya es mayor que${\displaystyle 2\uparrow ^{9}16}$. ^[42]

Referencias

1. Rudman, Peter S. (2009), Cómo sucedieron las matemáticas: los primeros 50.000 años , Prometheus Books, p. 148, ISBN 978-1-61592-176-8
2. Barnes, John (2016), Nice Numbers , Springer International Publishing, doi : 10.1007 / 978-3-319-46831-0 , Tenga en cuenta que las medidas binarias (2, 4, 8, 16) son muy comunes. Esto es particularmente obvio con los volúmenes.
3. Curtis, Lorenzo J. (1978), "Concepto de la ley exponencial antes de 1900", American Journal of Physics , 46 (9): 896–906, doi : 10.1119 / 1.11512
4. Miller, Heather M.-L. (2013), "Asuntos de peso: evidencia de unidad y diversidad regional de los pesos de la civilización del Indo", en Abraham, Shinu Anna; Gullapalli, Praveena; Raczek, Teresa P .; Rizvi, Uzma Z. (eds.), Conexiones y complejidad: Nuevos enfoques de la arqueología del sur de Asia , Left Coast Press, págs. 161-177, doi : 10.4324 / 9781315431857 , ISBN 978-1-59874-686-0; ver en particular p. 166
5. Kirk, David B .; Hwu, Wen-mei W. (2013), "7.2 Números representables" , Programación de procesadores masivamente paralelos: un enfoque práctico (2ª ed.), Morgan Kaufmann, págs. 155-159, ISBN 978-0-12-391418-7
6. Kneusel, Ronald T. (2017), "Capítulo 6: números de punto fijo", Números y computadoras (2.a ed.), Springer International Publishing, págs. 183-214, doi : 10.1007 / 978-3-319-50508 -4_6
7. van der Hoeven, Joris (2006), "Cálculos con números reales efectivos", Informática teórica , 351 (1): 52-60, doi : 10.1016 / j.tcs.2005.09.060 , MR 2201092 
8. Ko, Ker-I (1991), Teoría de la complejidad de las funciones reales , Progreso en la informática teórica, Boston, Massachusetts: Birkhäuser Boston, Inc., págs. 41–43, doi : 10.1007 / 978-1 -4684-6802-1 , ISBN 0-8176-3586-6, MR  1137517
9. Zheng, Xizhong; Rettinger, Robert (2004), "Computabilidad débil y representación de reales", Mathematical Logic Quarterly , 50 (4–5): 431–442, doi : 10.1002 / malq.200310110 , MR 2090389 
10. Ambos-Spies, Klaus; Zheng, Xizhong (2019), "Sobre las diferencias y sumas de números reales fuertemente enumerables", en Manea, Florin; Martin, Barnaby; Paulusma, Daniël; Primiero, Giuseppe (eds.), Computing with Foresight and Industry: 15th Conference on Computability in Europe, CiE 2019, Durham, Reino Unido, 15-19 de julio de 2019, Actas , Lecture Notes in Computer Science, 11558 , Cham: Springer, págs. 310–322, doi : 10.1007 / 978-3-030-22996-2_27 , MR 3981892 
11. Jerrum, Mark R .; Valiant, Leslie G .; Vazirani, Vijay V. (1986), "Generación aleatoria de estructuras combinatorias a partir de una distribución uniforme", Informática teórica , 43 (2-3): 169-188, doi : 10.1016 / 0304-3975 (86) 90174-X , Señor 0855970 
12. Jones, Shelly M .; Pearson, Dunn (mayo de 2013), "Música: los estudiantes muy comprometidos conectan la música con las matemáticas", General Music Today , 27 (1): 18–23, doi : 10.1177 / 1048371313486478
13. Libbey, Theodore (2006), "Time signature" , Enciclopedia de música clásica de The NPR Listener , Workman Publishing, p. 873, ISBN 978-0-7611-2072-8
14. Yanakiev, Ivan K. (2020), "Dispositivos matemáticos en ayuda de la teoría musical, la composición y la interpretación", en Bozhikova, Milena (ed.), Music between Ontology and Ideology , Cambridge Scholars Publishing, págs. 35-62, ISBN 978-1-5275-4758-2; ver en particular p. 37 .
15. Hiebert, James; Tonnessen, Lowell H. (noviembre de 1978), "Desarrollo del concepto de fracción en dos contextos físicos: una investigación exploratoria", Journal for Research in Mathematics Education , 9 (5): 374–378, doi : 10.2307 / 748774 , JSTOR 748774 
16. Pothier, Yvonne ; Sawada, Daiyo (noviembre de 1983), "Particionamiento: el surgimiento de ideas de números racionales en niños pequeños", Journal for Research in Mathematics Education , 14 (5): 307–317, doi : 10.2307 / 748675 , JSTOR 748675 
17. Wells, David Graham (2015), Motivar las matemáticas: maestros y estudiantes comprometidos , World Scientific, págs. 32-33, ISBN 978-1-78326-755-2
18. Fórmulas equivalentes a éstas, escritas en el lenguaje deldemostrador de teoremas interactivo Coq , las da Krebbers, Robbert; Spitters, Bas (2013), "Clases de tipos para aritmética real exacta eficiente en Coq", Métodos lógicos en informática , 9 (1): 1:01, 27, arXiv : 1106.3448 , doi : 10.2168 / LMCS-9 (1: 1) 2013 , MR 3029087 
19. O'Connor, Russell (2007), "Una implementación monádica y funcional de números reales", Estructuras matemáticas en informática , 17 (1): 129-159, doi : 10.1017 / S0960129506005871 , MR 2311089 
20. Sabin, Malcolm (2010), Análisis y diseño de esquemas de subdivisión univariante , geometría y computación, 6 , Springer, p. 51, ISBN 9783642136481
21. Nilsson, Johan (2009), "Sobre números mal aproximados por racionales diádicos", Israel Journal of Mathematics , 171 : 93-110, doi : 10.1007 / s11856-009-0042-9 , MR 2520103 
22. Kac, Mark (1959), Independencia estadística en probabilidad, análisis y teoría de números , Carus Mathematical Monographs , 12 , Nueva York: John Wiley & Sons para la Asociación Matemática de América, págs. 2-3, MR 0110114 
23. Pollen, David (1992), "Función de escala de Daubechies en [0,3]", Wavelets , Wavelet Anal. Appl., 2 , Boston, Massachusetts: Academic Press, págs. 3-13, MR 1161245 
24. Bajnok, Béla (2013), Una invitación a las matemáticas abstractas , Nueva York: Springer, p. 186, doi : 10.1007 / 978-1-4614-6636-9
25. En la notación de Estes y Ohm para anillos que son ambos subanillos de${\displaystyle \mathbb {Q} }$ y anulaciones de ${\displaystyle \mathbb {Z} }$, los racionales diádicos son el anillo ${\displaystyle \mathbb {Z} _{\{2\}}}$. Consulte la sección 7 de Estes, Dennis; Ohm, Jack (1967), "Rango estable en anillos conmutativos" (PDF) , Journal of Algebra , 7 : 343–362, doi : 10.1016 / 0021-8693 (67) 90075-0 , MR 0217052  
26. Lucyshyn-Wright, Rory BB (2018), "Espacios convexos, espacios afines y conmutadores para teorías algebraicas", Estructuras categóricas aplicadas , 26 (2): 369–400, arXiv : 1603.03351 , doi : 10.1007 / s10485-017- 9496-9 , MR 3770912 
27. Manners, Freddie (2015), "Una solución al problema del pijama", Inventiones Mathematicae , 202 (1): 239-270, arXiv : 1305.1514 , doi : 10.1007 / s00222-014-0571-7 , MR 3402799 ; consulte la sección 6.2.1, "Un caso modelo:${\displaystyle {\widehat {\mathbb {Z} [1/2]}}}$", págs. 255-257.
28. Robert, Alain M. (2000), "5.4 Partes integrales y fraccionarias de${\displaystyle p}$-adic numbers ", un curso en${\displaystyle p}$-adic Analysis , Textos de posgrado en matemáticas, 198 , Nueva York: Springer-Verlag, págs. 40–43, doi : 10.1007 / 978-1-4757-3254-2 , ISBN 0-387-98669-3, MR  1760253
29. de Cornulier, Yves; Guyot, Luc; Pitsch, Wolfgang (2007), "Sobre los puntos aislados en el espacio de los grupos" (PDF) , Journal of Algebra , 307 (1): 254–277, arXiv : math / 0511714 , doi : 10.1016 / j.jalgebra.2006.02 0.012 , MR 2278053  
30. Nadler, SB Jr. (1973), "La indecomponibilidad del solenoide diádico", American Mathematical Monthly , 80 (6): 677-679, doi : 10.2307 / 2319174 , JSTOR 2319174 
31. Bhattacharjee, Meenaxi; Macpherson, Dugald; Möller, Rögnvaldur G .; Neumann, Peter M. (1997), "Números racionales", Notas sobre grupos de permutación infinita , Textos y lecturas en matemáticas, 12 , Berlín: Springer-Verlag, págs. 77-86, doi : 10.1007 / 978-93-80250- 91-5_9 , ISBN 81-85931-13-5, MR  1632579
32. Girgensohn, Roland (1996), "Construcción de funciones singulares a través de fracciones de Farey", Journal of Mathematical Analysis and Applications , 203 (1): 127-141, doi : 10.1006 / jmaa.1996.0370 , MR 1412484 
33. Cvitanović, Predrag; Gunaratne, Gemunu H .; Procaccia, Itamar (1988), "Propiedades topológicas y métricas de atractores extraños de tipo Hénon", Physical Review A , Third Series, 38 (3): 1503-1520, doi : 10.1103 / PhysRevA.38.1503 , MR 0970237 
34. Brin, Matthew G. (1999), "La ubicuidad del grupo F de Thompson en grupos de homeomorfismos lineales por partes del intervalo unitario", Revista de la Sociedad Matemática de Londres , Segunda Serie, 60 (2): 449-460, arXiv : matemáticas / 9705205 , doi : 10.1112 / S0024610799007905 , MR 1724861 
35. Cannon, JW ; Floyd, WJ (2011), "¿Qué es ... el grupo de Thompson?" (PDF) , Notices of the American Mathematical Society , 58 (8): 1112-1113, MR 2856142  
36. Fernandes, António M .; Ferreira, Fernando (2005), "Aplicaciones básicas del lema de König débil en el análisis factible" (PDF) , Reverse Mathematics 2001 , Lecture Notes in Logic, 21 , La Jolla, California: Association for Symbolic Logic, pp. 175-188, MR 2185433  
37. Conway, JH (2001), Sobre números y juegos (Segunda ed.), Natick, Massachusetts: AK Peters, ISBN 1-56881-127-6, MR  1803095; para los racionales diádicos, consulte "Los números${\displaystyle {\tfrac {1}{4}}}$, ${\displaystyle {\tfrac {3}{4}}}$, ${\displaystyle 1\,{\tfrac {1}{2}}}$, ${\displaystyle 3}$, etc. ", págs. 10-12
38. Mauldon, JG (1978), "Num, a variant of Nim with no first-player win", American Mathematical Monthly , 85 (7): 575–578, doi : 10.2307 / 2320870 , JSTOR 2320870 , MR 0503877  
39. Flanigan, JA (1982), "Un análisis completo de Hackendot en blanco y negro", International Journal of Game Theory , 11 (1): 21-25, doi : 10.1007 / BF01771244 , MR 0665515 
40. Uiterwijk, Jos WHM; Barton, Michael (2015), "Nuevos resultados para Domineering a partir de bases de datos de finales de juego de teoría combinatoria", Theoretical Computer Science , 592 : 72-86, arXiv : 1506.03949 , doi : 10.1016 / j.tcs.2015.05.017 , MR 3367582 
41. Erickson, Jeff; Nivasch, Gabriel; Xu, Junyan (junio de 2021), "Números fusibles y aritmética de Peano" , Actas del 36 ° Simposio anual ACM / IEEE sobre lógica en informática (LICS 2021) , IEEE, págs. 1-13, arXiv : 2003.14342 , doi : 10.1109 /lics52264.2021.9470703
42. Sloane, N. J. A. (ed.), "Secuencia A188545" , La enciclopedia en línea de secuencias de enteros , Fundación OEIS