Ecuación de difracción de Fraunhofer

Explicación matemática de la difracción de campo lejano

En óptica , la ecuación de difracción de Fraunhofer se usa para modelar la difracción de ondas cuando el patrón de difracción se ve a una gran distancia del objeto difractante, y también cuando se ve en el plano focal de una lente de imagen . ^{[1] [2]}

La ecuación fue nombrada en honor a Joseph von Fraunhofer, aunque en realidad no participó en el desarrollo de la teoría. ^[3]

Este artículo presenta la ecuación en varias formas matemáticas y proporciona cálculos detallados del patrón de difracción de Fraunhofer para varias formas diferentes de aperturas de difracción, especialmente para ondas planas monocromáticas normalmente incidentes. Una discusión cualitativa de la difracción de Fraunhofer se puede encontrar en otra parte .

Definición

Cuando un haz de luz está parcialmente bloqueado por un obstáculo, parte de la luz se dispersa alrededor del objeto y, a menudo, se ven bandas claras y oscuras en el borde de la sombra; este efecto se conoce como difracción. ^[4] La ecuación de difracción de Kirchhoff proporciona una expresión, derivada de la ecuación de onda , que describe la onda difractada por una apertura; Las soluciones analíticas para esta ecuación no están disponibles para la mayoría de las configuraciones. ^[5]

La ecuación de difracción de Fraunhofer es una aproximación que se puede aplicar cuando la onda difractada se observa en el campo lejano , y también cuando se usa una lente para enfocar la luz difractada; en muchos casos, se dispone de una solución analítica simple para la ecuación de Fraunhofer; varias de ellas se derivan a continuación.

En coordenadas cartesianas

Geometría de difracción, que muestra el plano de apertura (u objeto difractante) y el plano de la imagen, con sistema de coordenadas.

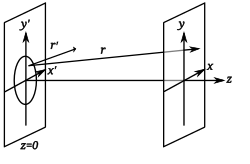
Si la apertura está en el plano x'y ' , con el origen en la apertura y está iluminada por una onda monocromática , de longitud de onda λ, número de onda k con amplitud compleja A ( x ', y ') , y la onda difractada se observa en el plano x, y, z donde l , m son los cosenos de dirección del punto x, y con respecto al origen, la amplitud compleja U ( x , y )de la onda difractada viene dada por la ecuación de difracción de Fraunhofer como: ^[6]

${\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}}\,A(x',y')e^{-i{\frac {2\pi }{\lambda }}(lx'+my')}\,dx'\,dy'}$

${\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}}\,A(x',y')e^{-ik(lx'+my')}\,dx'\,dy'}$

A partir de esta ecuación se puede ver que la forma del patrón de difracción depende solo de la dirección de visión, por lo que el patrón de difracción cambia de tamaño pero no de forma con el cambio de la distancia de visión.

La ecuación de difracción de Fraunhofer se puede expresar en una variedad de formas matemáticamente equivalentes. Por ejemplo: ^[7]

${\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}}\,A(x',y')e^{-i{\frac {2\pi }{\lambda z}}(x'x+y'y)}\,dx'\,dy'}$

${\displaystyle U(x,y,z)\propto \iint _{\text{Aperture}}\,A(x',y')e^{-i{\frac {k(x'x+y'y)}{z}}}\,dx'\,dy'}$

Puede verse que la integral en las ecuaciones anteriores es la transformada de Fourier de la función de apertura evaluada en frecuencias ^[8]

${\displaystyle f_{x}=x/(\lambda z)=l/\lambda }$

${\displaystyle f_{y}=y/(\lambda z)=m/\lambda }$

Por lo tanto, también podemos escribir la ecuación en términos de una transformada de Fourier como:

${\displaystyle U(x,y,z)\propto {\hat {f}}[A(x',y')]_{f_{x}f_{y}}}$

donde  es la transformada de Fourier de una . La formulación de la transformada de Fourier puede ser muy útil para resolver problemas de difracción.

Otra forma es:

${\displaystyle U(\mathbf {r} )\propto {\int _{\text{Aperture}}A(\mathbf {r'} )e^{-i\mathbf {k} \cdot (\mathbf {r'} -\mathbf {r} )}dr'}={\int _{\text{Aperture}}a_{0}(\mathbf {r'} )e^{i\mathbf {(k_{0}-k)} \cdot (\mathbf {r'} -\mathbf {r} )}dr'}}$

donde r y r ' representar el punto de observación y un punto en la abertura respectivamente, k ₀ y k representan los vectores de onda de la perturbación en la abertura y de las olas difractados respectivamente, y un ₀ ( r' ) representa la magnitud de la perturbación en la apertura.

En coordenadas polares

Cuando la apertura de difracción tiene simetría circular, es útil utilizar coordenadas polares en lugar de cartesianas . ^[9]

Un punto en la apertura tiene coordenadas ρ , ω dando:

${\displaystyle ~x'=\rho '\cos \omega ';y'=\rho '\sin \omega '}$

y

${\displaystyle ~x=\rho \cos \omega ;y=\rho \sin \omega }$

La amplitud compleja en ρ ' viene dada por A (ρ) , y el área d x d y se convierte en ρ ′ d ρ ′ d ω ′ , dando

${\displaystyle {\begin{aligned}U(\rho ,\omega ,z)&\propto \int _{0}^{\infty }\int _{0}^{2\pi }A(\rho ')e^{-i{\frac {2\pi }{\lambda z}}(\rho \rho '\cos \omega \cos \omega '+\rho \rho '\sin \omega \sin \omega ')}\rho 'd\rho 'd\omega '\\&\propto \int _{0}^{2\pi }\int _{0}^{\infty }A(\rho ')e^{-i{\frac {2\pi }{\lambda z}}\rho \rho '\cos(\omega -\omega ')}\,d\omega '\rho '\,d\rho '\end{aligned}}}$

Usando la representación integral de la función de Bessel : ^[10]

${\displaystyle J_{0}(p)={\frac {1}{2\pi }}\int _{0}^{2\pi }e^{ip\cos \alpha }\,d\alpha }$

tenemos

${\displaystyle {\begin{aligned}U(\rho ,z)&\propto 2\pi \int _{0}^{\infty }A(\rho ')J_{0}\left({\frac {2\pi \rho '\rho }{\lambda z}}\right)\rho '\,d\rho '\end{aligned}}}$

donde la integración sobre ω da 2 π ya que la ecuación es circularmente simétrica, es decir, no hay dependencia de ω .

En este caso, tenemos U ( ρ , z ) igual a la transformada de Fourier-Bessel o Hankel de la función de apertura, A ( ρ )

Ejemplo

Aquí se dan ejemplos de difracción de Fraunhofer con una onda plana monocromática normalmente incidente.

En cada caso, el objeto difractante está ubicado en el  plano z = 0, y la amplitud compleja de la onda del plano incidente está dada por

${\displaystyle ~A(x',y')=ae^{i2\pi ct/\lambda }=ae^{ikct}}$

donde

a es la magnitud de la perturbación de las olas,

λ es la longitud de onda,

c es la velocidad de la luz,

t es el tiempo

k = 2 π / λ es el número de onda

y la fase es cero en el tiempo t = 0.

El factor dependiente del tiempo se omite en todos los cálculos, ya que permanece constante y se promedia cuando se calcula la intensidad . La intensidad en r es proporcional a la amplitud multiplicada por su conjugado complejo

${\displaystyle I(\mathbf {r} )\propto U(\mathbf {r} ){\overline {U}}(\mathbf {r} )}$

Estas derivaciones se pueden encontrar en la mayoría de los libros de óptica estándar, en formas ligeramente diferentes utilizando notaciones variables. Se da una referencia para cada uno de los sistemas modelados aquí. Las transformadas de Fourier utilizadas se pueden encontrar aquí .

Rendija rectangular estrecha

Gráfico e imagen de difracción de una sola rendija

La apertura es una rendija de ancho W que se encuentra a lo largo del eje y ,

Solución por integración

Suponiendo que el centro de la rendija está ubicado en x = 0 , la primera ecuación anterior, para todos los valores de y , es: ^[11]

${\displaystyle {\begin{aligned}U(x,z)&=a\int _{-W/2}^{W/2}e^{{-2\pi ixx'}/(\lambda z)}\,dx'\\[4pt]&=-{\frac {a\lambda z}{2\pi ix}}\left|e^{{-2\pi ixx'}/(\lambda z)}\right|_{-W/2}^{W/2}\end{aligned}}}$

Usando la fórmula de Euler , esto se puede simplificar a:

${\displaystyle {\begin{aligned}U(x,z)&=aW{\frac {\sin \left[{\frac {\pi Wx}{\lambda z}}\right]}{\frac {\pi Wx}{\lambda z}}}\\&=aW\operatorname {sinc} {\frac {\pi Wx}{\lambda z}}\end{aligned}}}$

donde sinc ( p ) = sin ( p ) / p . La función sinc a veces se define como sin ( π p ) / π p y esto puede causar confusión al mirar derivaciones en diferentes textos.

Esto también se puede escribir como:

${\displaystyle U(\theta )=aW\operatorname {sinc} \left[{\frac {\pi W\sin \theta }{\lambda }}\right]}$

donde θ es el ángulo entre el eje z y la línea que une x con el origen y sin θ ≈ x / z cuando θ << 1 .

Solución de transformada de Fourier

La rendija se puede representar mediante la función rect como: ^[12]

${\displaystyle ~\operatorname {rect} \left({\frac {x}{W}}\right)}$

La transformada de Fourier de esta función está dada por

${\displaystyle {\hat {f}}(\operatorname {rect} (ax))=\displaystyle {\frac {1}{|a|}}\cdot \operatorname {sinc} \left({\frac {\xi }{a}}\right)}$

donde ξ es la frecuencia de la transformada de Fourier, y la función sinc se define aquí como sin ( π x ) / ( π x )

La frecuencia de la transformada de Fourier aquí es x / λz , dando

${\displaystyle {\begin{aligned}U(x,z)&\propto W{\frac {\sin {\frac {\pi Wx}{\lambda z}}}{\frac {\pi Wx}{\lambda z}}}\\&\propto W\operatorname {sinc} {\frac {\pi Wx}{\lambda z}}\\&\propto W\operatorname {sinc} {\frac {\pi W\sin \theta }{\lambda }}\\&\propto W\operatorname {sinc} (kW\sin \theta /2)\end{aligned}}}$

Tenga en cuenta que la función sinc se define aquí como sin ( x ) / ( x ) para mantener la coherencia.

Intensidad

La intensidad es proporcional al cuadrado de la amplitud y, por tanto, es ^[13]

${\displaystyle {\begin{aligned}I(\theta )&\propto \operatorname {sinc} ^{2}\left[{\frac {\pi W\sin \theta }{\lambda }}\right]\\&\propto \operatorname {sinc} ^{2}\left[{\frac {kW\sin \theta }{2}}\right]\end{aligned}}}$

Aberturas

Apertura rectangular

Simulación por computadora de la difracción de Fraunhofer por una apertura rectangular

Cuando una rendija de ancho W y alto H es iluminada normalmente por una onda plana monocromática de longitud de onda λ, la amplitud compleja se puede encontrar usando análisis similares a los de la sección anterior, aplicados sobre dos dimensiones independientes como: ^{[14] [15]}

${\displaystyle {\begin{aligned}U(\theta ,\phi )&\propto \operatorname {sinc} \left({\frac {\pi W\sin \theta }{\lambda }}\right)\operatorname {sinc} \left({\frac {\pi H\sin \phi }{\lambda }}\right)\\&\propto \operatorname {sinc} \left({\frac {kW\sin \theta }{2}}\right)\operatorname {sinc} \left({\frac {kH\sin \phi }{2}}\right)\end{aligned}}}$

La intensidad viene dada por

${\displaystyle {\begin{aligned}I(\theta ,\phi )&\propto \operatorname {sinc} ^{2}\left({\frac {\pi W\sin \theta }{\lambda }}\right)\operatorname {sinc} ^{2}\left({\frac {\pi H\sin \phi }{\lambda }}\right)\\&\propto \operatorname {sinc} ^{2}\left({\frac {kW\sin \theta }{2}}\right)\operatorname {sinc} ^{2}\left({\frac {kH\sin \phi }{2}}\right)\end{aligned}}}$

donde θ y φ son los ángulos entre la x y z ejes y la Y y Z ejes, respectivamente.

En la práctica, todas las rendijas son de longitud finita y, por tanto, producirán difracción en ambas direcciones. Si la longitud de la rendija es mucho mayor que su ancho, entonces el espaciado de las franjas de difracción horizontal será mucho menor que el espaciado de las franjas verticales. Si el rayo de iluminación no ilumina toda la longitud de la rendija, la separación de las franjas horizontales está determinada por las dimensiones del rayo láser. Un examen detenido del patrón de dos rendijas a continuación muestra que hay franjas de difracción horizontales muy finas por encima y por debajo del punto principal, así como franjas verticales más obvias.

Apertura circular

Patrón de difracción aireado

La abertura tiene un diámetro W . La amplitud compleja en el plano de observación viene dada por

${\displaystyle {\begin{aligned}U(\rho ,z)&=2\pi a\int _{0}^{W/2}J_{0}\left({\frac {2\pi \rho '\rho }{\lambda z}}\right)\rho '\,d\rho '\end{aligned}}}$

Solución por integración

Usando la relación de recurrencia ^[16]

${\displaystyle {\frac {d}{dx}}\left[x^{n+1}J_{n+1}(x)\right]=x^{n+1}J_{n}(x)}$

dar

${\displaystyle \int _{0}^{x}x'J_{0}(x')\,dx'=xJ_{1}(x)}$

Si sustituimos

${\displaystyle x'={\frac {2\pi \rho }{\lambda z}}\rho '}$

y los límites de la integración se vuelven 0 y πρW / λz , obtenemos

${\displaystyle U(\rho ,z)\propto {\frac {J_{1}(\pi W\rho /\lambda z)}{\pi W\rho /\lambda z}}}$

Poniendo ρ / z = sin  θ , obtenemos

${\displaystyle U(\theta )\propto {\frac {J_{1}(\pi W\sin \theta /\lambda )}{\pi W\sin \theta /\lambda }}}$

Solución usando la transformada de Fourier-Bessel

Podemos escribir la función de apertura como una función de paso.

${\displaystyle ~\Pi (W/2)}$

La transformada de Fourier-Bessel para esta función viene dada por la relación

${\displaystyle ~F[\Pi (r/a)]={\frac {2\pi J_{1}(qa)}{q}}}$

donde q / 2π es la frecuencia de transformación que es igual a ρ / λ z y a = W / 2 .

Por lo tanto, obtenemos

${\displaystyle {\begin{aligned}U(\rho )&={\frac {2\pi J_{1}(\pi W\rho /\lambda z)}{2\pi W\rho /\lambda z}}\\&={\frac {2\pi J_{1}(\pi W\sin \theta /\lambda )}{W\sin \theta /\lambda }}\\&={\frac {2\pi J_{1}(kW\sin \theta /2)}{kW\sin \theta /2}}\end{aligned}}}$

Intensidad

La intensidad viene dada por: ^[17]

${\displaystyle {\begin{aligned}I(\theta )&\propto \left[{\frac {J_{1}(\pi W\sin \theta /\lambda )}{\pi W\sin \theta /\lambda )}}\right]^{2}\\&\propto \left[{\frac {J_{1}(kW\sin \theta /2)}{(kW\sin \theta /2)}}\right]^{2}\end{aligned}}}$

Forma del patrón de difracción

Esto se conoce como patrón de difracción de Airy.

El patrón difractado es simétrico con respecto al eje normal.

Apertura con perfil gaussiano

Intensidad de una onda plana difractada a través de una apertura con perfil gaussiano

Una apertura con perfil gaussiano, por ejemplo, una diapositiva fotográfica cuya transmisión tiene una variación gaussiana, de modo que la amplitud en un punto de la apertura ubicado a una distancia r ' del origen viene dada por

${\displaystyle A(\rho ')=\exp {\left(-\left[{\frac {\rho '}{\sigma }}\right]^{2}\right)}}$

donación

${\displaystyle U(\rho ,z)=2\pi a\int _{0}^{\infty }\exp {\left(-\left[{\frac {\rho '}{\sigma }}\right]^{2}\right)}J_{0}(2\pi \rho '\rho /\lambda z)\rho '\,d\rho '}$

Solución usando la transformada de Fourier-Bessel

La transformada de Fourier-Bessel o Hankel se define como

${\displaystyle F_{\nu }(k)=\int _{0}^{\infty }f(r)J_{\nu }(kr)\,r\,dr}$

donde J _ν es la función de Bessel del primer tipo de orden ν con ν ≥ −1/2.

La transformada de Hankel es

${\displaystyle F_{\nu }[e^{(ar)^{2}/2}]={\frac {e^{-k^{2}/2a^{2}}}{a^{2}}}}$

donación

${\displaystyle {\begin{aligned}U(\rho ,z)&\propto e^{-[{\frac {\pi \rho \sigma }{\lambda z}}]^{2}}\end{aligned}}}$

y

${\displaystyle U(\theta )\propto e^{-[{\frac {\pi \sigma \sin \theta }{\lambda }}]^{2}}}$

Intensidad

La intensidad viene dada por: ^[18]

${\displaystyle I(\theta )\propto e^{-[{\frac {2\pi \sigma \sin \theta }{\lambda }}]}}$

Esta función está graficada a la derecha y se puede ver que, a diferencia de los patrones de difracción producidos por aperturas rectangulares o circulares, no tiene anillos secundarios. Esto se puede utilizar en un proceso llamado apodización : la apertura está cubierta por un filtro cuya transmisión varía como una función gaussiana, dando un patrón de difracción sin anillos secundarios .: ^{[19] [20]}

Hendiduras

Dos rendijas

El patrón que ocurre cuando la luz difractada de dos rendijas se superpone es de considerable interés en física, en primer lugar por su importancia para establecer la teoría ondulatoria de la luz a través del experimento de interferencia de Young , y en segundo lugar debido a su papel como un experimento mental en el experimento de doble rendija en mecánica cuántica.

Hendiduras estrechas

Geometría de difracción de dos rendijas

Interferencia de dos rendijas usando un láser rojo

Suponga que tenemos dos rendijas largas iluminadas por una onda plana de longitud de onda λ . Las rendijas están en el plano z = 0 , paralelas al eje y , separadas por una distancia S y son simétricas con respecto al origen. El ancho de las rendijas es pequeño en comparación con la longitud de onda.

Solución por integración

La luz incidente es difractada por las rendijas en ondas esféricas uniformes. Las ondas que viajan en una dirección determinada θ desde las dos rendijas tienen fases diferentes. La fase de las ondas de las ranuras superior e inferior en relación con el origen está dada por (2π / λ) (S / 2) sin θ y - (2π / λ) (S / 2) sin θ

La amplitud compleja de las ondas sumadas viene dada por: ^[21]

${\displaystyle {\begin{aligned}U(\theta )&=ae^{\frac {i\pi S\sin \theta }{\lambda }}+ae^{-{\frac {i\pi S\sin \theta }{\lambda }}}\\&=a(\cos {\frac {\pi S\sin \theta }{\lambda }}+i\sin {\frac {\pi S\sin \theta }{\lambda }})+a(\cos {\frac {\pi S\sin \theta }{\lambda }}-i\sin {\frac {\pi S\sin \theta }{\lambda }})\\&=2a\cos {\frac {\pi S\sin \theta }{\lambda }}\end{aligned}}}$

Solución usando transformada de Fourier

La apertura se puede representar mediante la función: ^[22]

${\displaystyle ~a[\delta {(x-S/2)}+\delta {(x+S/2)}]}$

donde δ es la función delta .

Nosotros tenemos

${\displaystyle {\hat {f}}[\delta (x)]=1}$

y

${\displaystyle {\hat {f}}[g(x-a)]=e^{-2\pi iaf_{x}}{\hat {f}}[g(x)]}$

donación

${\displaystyle {\begin{aligned}U(x,z)&={\hat {f}}[\delta {(x-S/2)}+\delta {(x+S/2)}]\\&=e^{-i\pi Sx/2\lambda }+e^{i\pi Sx/2\lambda }\\&=2\cos {\frac {\pi Sx}{2\lambda }}\end{aligned}}}$

${\displaystyle U(\theta )=2\cos {\frac {\pi S\sin \theta }{2\lambda }}}$

Ésta es la misma expresión que la derivada anteriormente por integración.

Intensidad

Esto da la intensidad de las ondas combinadas como: ^[23]

${\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi S\sin \theta }{\lambda }}\right]\\&\propto \cos ^{2}{\left[{\frac {kS\sin \theta }{2}}\right]}\end{aligned}}}$

Hendiduras de ancho finito

Difracción de rendija simple y doble: la separación de la rendija es de 0,7 mm y el ancho de la rendija es de 0,1 mm

El ancho de las rendijas, W es finito.

Solución por integración

El patrón difractado viene dado por: ^[24]

${\displaystyle {\begin{aligned}U(\theta )&=a\left[e^{\frac {i\pi S\sin \theta }{\lambda }}+e^{-{\frac {i\pi S\sin \theta }{\lambda }}}\right]\int _{-W/2}^{W/2}e^{{-2\pi ix'\sin \theta }/(\lambda )}\,dx'\\&=2a\cos {\frac {\pi S\sin \theta }{\lambda }}W\operatorname {sinc} {\frac {\pi W\sin \theta }{\lambda }}\end{aligned}}}$

Solución usando transformada de Fourier

La función de apertura viene dada por: ^[25]

${\displaystyle a\left[\operatorname {rect} \left({\frac {x-S/2}{W}}\right)+\operatorname {rect} \left({\frac {x+S/2}{W}}\right)\right]}$

La transformada de Fourier de esta función está dada por

${\displaystyle {\hat {f}}(\operatorname {rect} (ax))=\displaystyle {\frac {1}{|a|}}\cdot \operatorname {sinc} \left({\frac {\xi }{a}}\right)}$

donde ξ es la frecuencia de la transformada de Fourier, y la función sinc se define aquí como sin ( πx ) / ( πx )

y

${\displaystyle {\hat {f}}[g(x-a)]=e^{-2\pi iaf_{x}}{\hat {f}}[g(x)]}$

Tenemos

${\displaystyle {\begin{aligned}U(x,z)&={\hat {f}}\left[a\left[\operatorname {rect} \left({\frac {x-S/2}{W}}\right)+\operatorname {rect} \left({\frac {x+S/2}{W}}\right)\right]\right]\\&=2W\left[e^{-i\pi Sx/\lambda z}+e^{i\pi Sx/\lambda z}\right]{\frac {\sin {\frac {\pi Wx}{\lambda z}}}{\frac {\pi Wx}{\lambda z}}}\\&=2a\cos {\frac {\pi Sx}{\lambda z}}W\operatorname {sinc} {\frac {\pi Wx}{\lambda z}}\end{aligned}}}$

o

${\displaystyle U(\theta )=2a\cos {\frac {\pi S\sin \theta }{\lambda }}W\operatorname {sinc} {\frac {\pi W\sin \theta }{\lambda }}}$

Esta es la misma expresión que se derivó por integración.

Intensidad

La intensidad viene dada por: ^[26]

${\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi S\sin \theta }{\lambda }}\right]\operatorname {sinc} ^{2}\left[{\frac {\pi W\sin \theta }{\lambda }}\right]\\&\propto \cos ^{2}\left[{\frac {kS\sin \theta }{2}}\right]\operatorname {sinc} ^{2}\left[{\frac {kW\sin \theta }{2}}\right]\end{aligned}}}$

Puede verse que la forma del patrón de intensidad es el producto del patrón de difracción de rendija individual y el patrón de interferencia que se obtendría con rendijas de ancho despreciable. Esto se ilustra en la imagen de la derecha que muestra la difracción de una sola rendija por un rayo láser, y también el patrón de difracción / interferencia dado por dos rendijas idénticas.

Rejillas

Una rejilla se define en Born y Wolf como "cualquier disposición que impone a una onda incidente una variación periódica de amplitud o fase, o ambas". ^[27]

Rejilla de hendidura estrecha

Una rejilla simple consiste de una pantalla con N ranuras cuya anchura es considerablemente menor que la longitud de onda de la luz incidente con una separación de hendidura de S .

Solución por integración

La amplitud compleja de la onda difractada en un ángulo θ viene dada por: ^[28]

${\displaystyle {\begin{aligned}U(\theta )&=a\sum _{n=1}^{N}e^{\frac {-i2\pi nS\sin \theta }{\lambda }}\\&={\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}}$

ya que esta es la suma de una serie geométrica .

Solución usando transformada de Fourier

La apertura viene dada por

${\displaystyle \sum _{n=0}^{N}\delta (x-nS)}$

La transformada de Fourier de esta función es: ^[29]

${\displaystyle {\begin{aligned}{\hat {f}}\left[\sum _{n=0}^{N}\delta (x-nS)\right]&=\sum _{n=0}^{N}e^{-if_{x}nS}\\&={\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}}$

Intensidad

Patrón de difracción para 50 rejillas de rendija estrecha

Detalle del máximo principal en patrones de difracción de rejilla de rendija estrecha de 20 y 50

La intensidad viene dada por: ^[30]

${\displaystyle {\begin{aligned}I(\theta )&\propto {\frac {1-\cos(2\pi NS\sin \theta /\lambda )}{1-\cos(2\pi S\sin \theta /\lambda )}}\\&\propto {\frac {\sin ^{2}(\pi NS\sin \theta /\lambda )}{\sin ^{2}(\pi S\sin \theta /\lambda )}}\end{aligned}}}$

Esta función tiene una serie de máximos y mínimos. Hay "máximos principales" espaciados regularmente, y un número de máximos mucho más pequeños entre los máximos principales. Los principales máximos ocurren cuando

${\displaystyle \pi S\sin _{n}\theta /\lambda =n\pi ,n=0,\pm 1,\pm 2,\ldots }$

y los principales haces difractados, por lo tanto, se producen en ángulos:

${\displaystyle \sin \theta _{n}={\frac {n\lambda }{S}},n=0,\pm 1\pm 2,\ldots }$

Ésta es la ecuación de rejilla para la luz incidente normalmente.

El número de pequeño maxima intermedio es igual al número de ranuras, N  - 1 y su tamaño y forma se determina también por N .

La forma del patrón para N = 50 se muestra en la primera figura.

La estructura detallada para rejillas de 20 y 50 ranuras se ilustra en el segundo diagrama.

Rejilla de hendidura de ancho finito

Patrón de difracción de la rejilla con ranuras de ancho finito

La rejilla ahora tiene N ranuras de ancho W y espaciado S

Solución mediante integración

La amplitud viene dada por: ^[31]

${\displaystyle {\begin{aligned}U(\theta ,\phi )&\propto a\sum _{n=1}^{N}e^{\frac {-i2\pi nS\sin \theta }{\lambda }}\int _{-W/2}^{W/2}e^{{-2\pi ixx'}/(\lambda z)}\,dx'\\&\propto a\operatorname {sinc} \left({\frac {\pi W\sin \theta }{\lambda }}\right){\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}}$

Solución usando transformada de Fourier

La función de apertura se puede escribir como: ^[32]

${\displaystyle \sum _{n=1}^{N}\operatorname {rect} \left[{\frac {x'-nS}{W}}\right]}$

Usando el teorema de convolución , que dice que si tenemos dos funciones f ( x ) y g ( x ) , y tenemos

${\displaystyle h(x)=(f*g)(x)=\int _{-\infty }^{\infty }f(y)g(x-y)\,dy,}$

donde ∗ denota la operación de convolución, entonces también tenemos

${\displaystyle {\hat {h}}(\xi )={\hat {f}}(\xi )\cdot {\hat {g}}(\xi ).}$

podemos escribir la función de apertura como

${\displaystyle \operatorname {rect} (x'/W)*\sum _{n=0}^{N}\delta (x'-nS)}$

La amplitud viene dada por la transformada de Fourier de esta expresión como:

${\displaystyle {\begin{aligned}U(x,z)&={\hat {f}}[\operatorname {rect} (x'/W)]{\hat {f}}\left[\sum _{n=0}^{N}\delta (x'-nS)\right]\\&=a\operatorname {sinc} \left({\frac {W\sin \theta }{\lambda }}\right){\frac {1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}}\end{aligned}}}$

Intensidad

La intensidad viene dada por: ^[33]

${\displaystyle {\begin{aligned}I(\theta )&\propto \operatorname {sinc} ^{2}\left({\frac {W\sin \theta }{\lambda }}\right){\frac {\sin ^{2}(\pi NS\sin \theta /\lambda )}{\sin ^{2}(\pi S\sin \theta /\lambda )}}\end{aligned}}}$

El diagrama muestra el patrón de difracción para una rejilla con 20 rendijas, donde el ancho de las rendijas es 1/5 de la separación de las rendijas. El tamaño de los picos difractados principales se modula con el patrón de difracción de las rendijas individuales.

Otras rejillas

El método de la transformada de Fourier anterior se puede utilizar para encontrar la forma de la difracción para cualquier estructura periódica donde se conoce la transformada de Fourier de la estructura. Goodman ^[34] utiliza este método para derivar expresiones para el patrón de difracción obtenido con rejillas de modulación de fase y amplitud sinusoidal. Estos son de particular interés en holografía .

Extensiones

Iluminación anormal

Si la apertura está iluminada por una onda plana monocromática incidente en una dirección ( l ₀ , m ₀ , n ₀ ) , la primera versión de la ecuación de Fraunhofer anterior se convierte en: ^[35]

${\displaystyle {\begin{aligned}U(x,y,z)&\propto \iint _{\text{Aperture}}\,A(x',y')e^{-i{\frac {2\pi }{\lambda }}[(l-l_{0})x'+(m-m_{0})y']}\,dx'\,dy'\\&\propto \iint _{\text{Aperture}}\,A(x',y')e^{-ik[(l-l_{0})x'+(m-m_{0})y']}\,dx'\,dy'\end{aligned}}}$

Las ecuaciones utilizadas para modelar cada uno de los sistemas anteriormente están alterados solamente por los cambios en las constantes de multiplicación de x y y , por lo que los patrones de luz difractados tendrán la forma, excepto que ahora se centra alrededor de la dirección de la onda plana incidente.

La ecuación de rejilla se convierte en ^[36]

${\displaystyle \sin \theta _{n}={\frac {n\lambda }{S}}+\sin \theta _{0},n=0,\pm 1,\pm 2,\ldots }$

Iluminación no monocromática

En todos los ejemplos anteriores de difracción de Fraunhofer, el efecto de aumentar la longitud de onda de la luz de iluminación es reducir el tamaño de la estructura de difracción y, a la inversa, cuando se reduce la longitud de onda, aumenta el tamaño del patrón. Si la luz no es monocromática, es decir, consta de un rango de longitudes de onda diferentes, cada longitud de onda se difracta en un patrón de tamaño ligeramente diferente al de sus vecinas. Si la extensión de las longitudes de onda es significativamente menor que la longitud de onda media, los patrones individuales variarán muy poco en tamaño y, por lo tanto, la difracción básica seguirá apareciendo con un contraste ligeramente reducido. A medida que aumenta la extensión de las longitudes de onda, se reduce el número de "franjas" que se pueden observar.

Ver también

• Fórmula de difracción de Kirchhoff
• Difracción de Fresnel
• Principio de Huygens
• Disco aireado
• Óptica de Fourier

Referencias

1. Nacido y lobo, 1999, p 427.
2. Jenkins y White, 1957, p 288
3. http://scienceworld.wolfram.com/biography/Fraunhofer.html
4. Cielos y Ditchburn, 1996, p 62
5. Nacido y lobo, 2002, p 425
6. Lipson et al., 2011, eq (8.8) p 231
7. Hecht, 2002, eq (11.63), p 529
8. Hecht, 2002, eq (11.67), p 540
9. Born & Wolf, 2002, sección 8.5.2, eqs (6–8), p 439
10. Abramowitz y Stegun, 1964, sección 9.1.21, p 360
11. Born & Wolf, 1999, sección 8.5.1 p 436
12. Hecht, 2002, p 540
13. Hecht, 2002, eqs (10.17) (10.18), p 453
14. Longhurst, 1967, p 217
15. Goodman, ecuación (4.28), p 76
16. Whittaker y Watson, ejemplo 2, p 360
17. Hecht, 2002, eq (10.56), p 469
18. Hecht, 2002, eq (11.2), p 521
19. Cielos y Ditchburn, 1991, p 68
20. Hecht, 2002, Figura (11.33), p 543
21. Jenkins y White, 1957, eq (16c), p 312
22. Hecht, 2002, eq (11.4328), p 5
23. Lipson et al., 2011, eq (9.3), p 280
24. Hecht, 2002, sección 10.2.2, p 451
25. Hecht, 2002, p 541
26. Jenkins y White, 1967, eq (16c), p 313
27. Born & Wolf, 1999, sección 8.6.1, p 446
28. Jenkins y White, 1957, eq (17a), p 330
29. Lipson et al., 2011, eq (4.41), p 106
30. Born & Wolf, 1999, eq (5a), p 448
31. Born & Wolf, sección 8.6.1, eq (5), p 448
32. Hecht, El teorema de la matriz, p 543
33. Born & Wolf, 2002, sección 8.6, eq (10), p 451
34. Goodman, 2005, Secciones 4.4.3 y 4.4.4, p 78
35. Lipson et al., 2011, Sección 8.2.2, p 232
36. Born & Wolf, 1999, eq (8), p 449

Fuentes de referencia

• Abramowitz Milton y Stegun Irene A, 1964, Dover Publications Inc, Nueva York.
• Born M & Wolf E, Principles of Optics , 1999, séptima edición, Cambridge University Press, ISBN  978-0-521-64222-4
• Goodman Joseph, 2005, Introducción a la óptica de Fourier, Roberts & Co. ISBN 0-9747077-2-4 o en línea aquí 
• Heavens OS y Ditchburn W, 1991, Insight into Optics, Longman and Sons, Chichester ISBN 978-0-471-92769-3 
• Hecht Eugene, Óptica, 2002, Addison Wesley, ISBN 0-321-18878-0 
• Jenkins FA & White HE, 1957, Fundamentals of Optics, 3rd Edition, McGraw Hill, Nueva York
• Lipson A, Lipson SG, Lipson H , 2011, Física óptica , 4a ed., Cambridge University Press, ISBN 978-0-521-49345-1 
• Longhurst RS, 1967, Óptica geométrica y física, 2a edición, Longmans, Londres
• Whittaker y Watson, 1962, Análisis moderno, Cambridge University Press.