Funciones elípticas de la lemniscata

En matemáticas , las funciones elípticas de la lemniscata son funciones elípticas relacionadas con la longitud del arco de la lemniscata de Bernoulli . Primero fueron estudiados por Giulio Fagnano en 1718 y luego por Leonhard Euler y Carl Friedrich Gauss , entre otros.

Las funciones lemniscata seno y lemniscata coseno , usualmente escritas con los símbolos sl y cl (a veces se usan los símbolos sinlem y coslem o sen lemn y cos lemn ) ^[1] son análogas a las funciones trigonométricas seno y coseno. Mientras que el seno trigonométrico relaciona la longitud del arco con la longitud de la cuerda en un círculo de diámetro unitario , el seno de la lemniscata relaciona la longitud del arco con la longitud de la cuerda de una lemniscata. ${\ Displaystyle x ^ {2} + y ^ {2} = x}$${\ Displaystyle {\ bigl (} x ^ {2} + y ^ {2} {\ bigr)} {} ^ {2} = x ^ {2} -y ^ {2}.}$

Las funciones de lemniscata tienen períodos relacionados con un número 2.622057 ... llamada constante de lemniscata , la relación entre el perímetro de una lemniscata y su diámetro.${\ Displaystyle \ varpi =}$

Los sl y cl funciones tienen un cuadrado período de celosía (un múltiplo de los enteros de Gauss ) con períodos fundamentales ^[2] y son un caso especial de dos funciones elípticas de Jacobi en que enrejado, .${\ Displaystyle \ {(1 + i) \ varpi, (1-i) \ varpi \},}$${\ Displaystyle \ operatorname {sl} z = \ operatorname {sn} (z; i),}$ ${\ Displaystyle \ operatorname {cl} z = \ operatorname {cd} (z; i)}$

De manera similar, las funciones de lemniscata hiperbólica slh y clh tienen un retículo de período cuadrado con períodos fundamentales${\ Displaystyle {\ bigl \ {} {\ sqrt {2}} \ varpi, {\ sqrt {2}} \ varpi i {\ bigr \}}.}$

Las funciones de lemniscata y las funciones de lemniscata hiperbólica están relacionadas con la función elíptica de Weierstrass .${\ Displaystyle \ wp (z; a, 0)}$

El seno de la lemniscata (rojo) y el coseno de la lemniscata (violeta) aplicados a un argumento real, en comparación con el seno trigonométrico y = sin ( πx / ϖ ) (rojo punteado pálido).

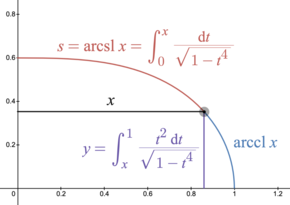
El seno y el coseno de la lemniscata relacionan la longitud del arco de un arco de la lemniscata con la distancia de un punto final desde el origen.

El seno y el coseno trigonométricos relacionan de manera análoga la longitud del arco de un arco de un círculo de diámetro unitario con la distancia de un punto final desde el origen.

El seno de la lemniscata relaciona la longitud del arco con la coordenada x en la elástica rectangular.

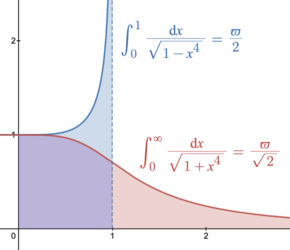
La constante de lemniscata es el doble del valor de la integral de lemniscata completa.

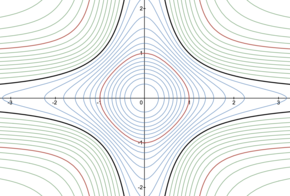
Curvas x ² ⊕ y ² = a para varios valores de a . Negativo una en verde, positivo una en azul, un = ± 1 en rojo, a = ∞ en negro.

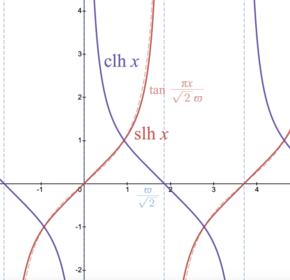
El seno de la lemniscata hiperbólica (rojo) y el coseno de la lemniscata hiperbólica (violeta) aplicados a un argumento real, en comparación con la tangente trigonométrica (rojo punteado pálido).

Con respecto a la curva de Fermat cuartica , el seno de la lemniscata hiperbólica es análoga a la función tangente trigonométrica.${\ Displaystyle x ^ {4} + y ^ {4} = 1}$

"El mundo en proyección quincuncial", de Peirce (1879).