número triangular al cuadrado
Esta identidad a veces se denomina teorema de Nicómaco , en honor a Nicómaco de Gerasa (c. 60 - c. 120 d. C.).
Nicomachus, al final del Capítulo 20 de su Introducción a la Aritmética , señaló que si uno escribe una lista de los números impares, el primero es el cubo de 1, la suma de los dos siguientes es el cubo de 2, la suma de los siguientes tres son el cubo de 3, y así sucesivamente. No va más allá, pero de aquí se sigue que la suma de los primeros n cubos es igual a la suma de los primeros números impares, es decir, los números impares del 1 al . El promedio de estos números es obviamente , y hay de ellos, por lo que su suma es
Muchos de los primeros matemáticos han estudiado y proporcionado pruebas del teorema de Nicómaco. Stroeker (1995) afirma que "todo estudiante de teoría de números seguramente debe haberse maravillado con este hecho milagroso". Pengelley (2002) encuentra referencias a la identidad no solo en las obras de Nicomachus en lo que ahora es Jordania en el siglo I EC, sino también en las de Aryabhata en India en el siglo V, y en las de Al-Karaji alrededor del año 1000 en persia _ Bressoud (2004) menciona varios trabajos matemáticos tempranos adicionales sobre esta fórmula, por Al-Qabisi (siglo X Arabia), Gersonides(circa 1300 Francia) y Nilakantha Somayaji (circa 1500 India); reproduce la prueba visual de Nilakantha.
Estos números pueden verse como números figurados , una generalización hiperpiramidal de cuatro dimensiones de los números triangulares y los números piramidales cuadrados .
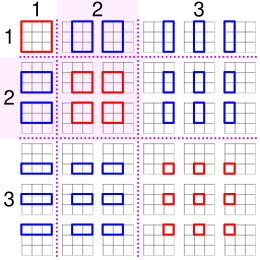
Como observa Stein (1971) , estos números también cuentan el número de rectángulos con lados horizontales y verticales formados en una cuadrícula n × n . Por ejemplo, los puntos de una cuadrícula de 4 × 4 (o un cuadrado formado por tres cuadrados más pequeños de un lado) pueden formar 36 rectángulos diferentes. El número de cuadrados en una cuadrícula cuadrada se cuenta de manera similar por los números piramidales cuadrados.