lema de sperner
En matemáticas , el lema de Sperner es un resultado combinatorio sobre coloraciones de triangulaciones , análogo al teorema del punto fijo de Brouwer , que es equivalente a él. [1] Establece que cada coloración de Sperner (descrita a continuación) de una triangulación de un símplex bidimensional contiene una celda cuyos vértices tienen colores diferentes.
El resultado inicial de este tipo fue probado por Emanuel Sperner , en relación con las pruebas de invariancia de dominio . Los colorantes de Sperner se han utilizado para el cálculo efectivo de puntos fijos y en algoritmos de búsqueda de raíces , y se aplican en algoritmos de división justa (corte de torta). Ahora se cree que encontrar una coloración de Sperner o, de manera equivalente, un punto fijo de Brouwer es un problema computacional intratable, incluso en el plano, en el caso general. El problema es PPAD-complete , una clase de complejidad inventada por Christos Papadimitriou .
Según la Enciclopedia Matemática Soviética (ed. IM Vinogradov ), un teorema relacionado de 1929 (de Knaster , Borsuk y Mazurkiewicz ) también se conoció como el lema de Sperner ; este punto se discute en la traducción al inglés (ed. M. Hazewinkel). Ahora se conoce comúnmente como el lema de Knaster-Kuratowski-Mazurkiewicz .
En una dimensión, el Lema de Sperner se puede considerar como una versión discreta del teorema del valor intermedio . En este caso, esencialmente dice que si una función discreta toma solo los valores 0 y 1, comienza en el valor 0 y termina en el valor 1, entonces debe cambiar de valor un número impar de veces.
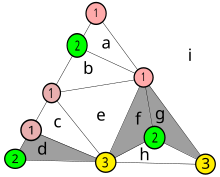
Subdividir un triángulo ABC arbitrariamente en una triangulación que consta de triángulos más pequeños que se encuentran borde con borde. Luego, una coloración de Sperner de la triangulación se define como una asignación de tres colores a los vértices de la triangulación tal que
Luego, cada coloración de Sperner de cada triangulación tiene al menos un "triángulo arcoíris", un triángulo más pequeño en la triangulación que tiene sus vértices coloreados con los tres colores diferentes. Más precisamente, debe haber un número impar de triángulos de arcoíris.