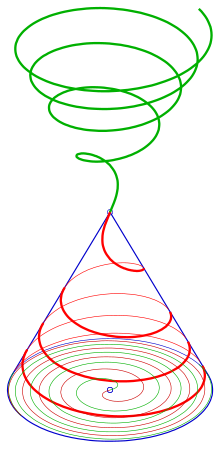
Espiral cónica

Espiral cónica con una espiral de Arquímedes como planta

plano de planta: espiral de Fermat

plano de planta: espiral logarítmica

plano de planta: espiral hiperbólica

En matemáticas, una espiral cónica es una curva sobre un cono circular recto , cuya planta es una espiral plana . Si el plano del piso es una espiral logarítmica , se llama concospiral (de concha ).

Las concospirales se utilizan en biología para modelar conchas de caracoles y trayectorias de vuelo de insectos ^{[1] [2]} y en ingeniería eléctrica para la construcción de antenas . ^{[3] [4]}

Representación paramétrica

En el plano - una espiral con representación paramétrica${\displaystyle x}$${\displaystyle y}$

${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

Se puede agregar una tercera coordenada de modo que la curva espacial se encuentre en el cono con la ecuación  :${\displaystyle z(\varphi )}$${\displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ m>0\;}$

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .}$

Estas curvas se denominan espirales cónicas. ^[5] Pappos los conocía .

El parámetro es la pendiente de las líneas del cono con respecto al plano - .${\displaystyle m}$${\displaystyle x}$${\displaystyle y}$

En cambio, una espiral cónica puede verse como la proyección ortogonal de la espiral del plano del piso sobre el cono.

Ejemplos de

1) Comenzar con una espiral de Arquímedes da como resultado la espiral cónica (ver diagrama)${\displaystyle \;r(\varphi )=a\varphi \;}$

${\displaystyle x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .}$

En este caso, la espiral cónica puede verse como la curva de intersección del cono con un helicoide .

2) El segundo diagrama muestra una espiral cónica con una espiral de Fermat como planta.${\displaystyle \;r(\varphi )=\pm a{\sqrt {\varphi }}\;}$

3) El tercer ejemplo tiene una espiral logarítmica como planta. Su característica especial es su pendiente constante (ver más abajo).${\displaystyle \;r(\varphi )=ae^{k\varphi }\;}$

La introducción de la abreviatura da la descripción: .${\displaystyle K=e^{k}}$${\displaystyle r(\varphi )=aK^{\varphi }}$

4) El ejemplo 4 se basa en una espiral hiperbólica . Tal espiral tiene una asíntota (línea negra), que es el plano de una hipérbola (púrpura). La espiral cónica se acerca a la hipérbola para .${\displaystyle \;r(\varphi )=a/\varphi \;}$${\displaystyle \varphi \to 0}$

Propiedades

La siguiente investigación trata sobre espirales cónicas de la forma y , respectivamente.${\displaystyle r=a\varphi ^{n}}$${\displaystyle r=ae^{k\varphi }}$

Pendiente

Ángulo de pendiente en un punto de una espiral cónica

La pendiente en un punto de una espiral cónica es la pendiente de la tangente de este punto con respecto al plano - . El ángulo correspondiente es su ángulo de pendiente (ver diagrama):${\displaystyle x}$${\displaystyle y}$

${\displaystyle \tan \beta ={\frac {z'}{\sqrt {(x')^{2}+(y')^{2}}}}={\frac {mr'}{\sqrt {(r')^{2}+r^{2}}}}\ .}$

Una espiral con da:${\displaystyle r=a\varphi ^{n}}$

• ${\displaystyle \tan \beta ={\frac {mn}{\sqrt {n^{2}+\varphi ^{2}}}}\ .}$

Porque una espiral de Arquímedes es y, por tanto, su pendiente es${\displaystyle n=1}$${\displaystyle \ \tan \beta ={\tfrac {m}{\sqrt {1+\varphi ^{2}}}}\ .}$

• Para una espiral logarítmica con pendiente es ( ).${\displaystyle r=ae^{k\varphi }}$${\displaystyle \ \tan \beta ={\tfrac {mk}{\sqrt {1+k^{2}}}}\ }$${\displaystyle \color {red}{\text{ constant!}}}$

Debido a esta propiedad, una concospiral se llama espiral cónica equiangular .

Longitud de arco

La longitud de un arco de una espiral cónica se puede determinar mediante

${\displaystyle L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(x')^{2}+(y')^{2}+(z')^{2}}}\,\mathrm {d} \varphi =\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(1+m^{2})(r')^{2}+r^{2}}}\,\mathrm {d} \varphi \ .}$

Para una espiral de Arquímedes, la integral se puede resolver con la ayuda de una tabla de integrales , de manera análoga al caso plano:

${\displaystyle L={\frac {a}{2}}{\big [}\varphi {\sqrt {(1+m^{2})+\varphi ^{2}}}+(1+m^{2})\ln {\big (}\varphi +{\sqrt {(1+m^{2})+\varphi ^{2}}}{\big )}{\big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}$

Para una espiral logarítmica, la integral se puede resolver fácilmente:

${\displaystyle L={\frac {\sqrt {(1+m^{2})k^{2}+1}}{k}}(r{\big (}\varphi _{2})-r(\varphi _{1}){\big )}\ .}$

En otros casos, ocurren integrales elípticas .

Desarrollo

Desarrollo (verde) de una espiral cónica (rojo), derecha: vista lateral. El avión que contiene el desarrollo está diseñado por . Inicialmente, el cono y el plano tocan la línea violeta.${\displaystyle \pi }$

Para el desarrollo de una espiral cónica ^{[6], es necesario determinar} la distancia de un punto de curva al vértice del cono y la relación entre el ángulo y el ángulo correspondiente del desarrollo:${\displaystyle \rho (\varphi )}$${\displaystyle (x,y,z)}$${\displaystyle (0,0,z_{0})}$${\displaystyle \varphi }$${\displaystyle \psi }$

${\displaystyle \rho ={\sqrt {x^{2}+y^{2}+(z-z_{0})^{2}}}={\sqrt {1+m^{2}}}\;r\ ,}$

${\displaystyle \varphi ={\sqrt {1+m^{2}}}\psi \ .}$

Por tanto, la representación polar de la espiral cónica desarrollada es:

• ${\displaystyle \rho (\psi )={\sqrt {1+m^{2}}}\;r({\sqrt {1+m^{2}}}\psi )}$

En el caso de la representación polar de la curva desarrollada es${\displaystyle r=a\varphi ^{n}}$

${\displaystyle \rho =a{\sqrt {1+m^{2}}}^{\,n+1}\psi ^{n},}$

que describe una espiral del mismo tipo.

• Si la planta de una espiral cónica es una espiral de Arquímedes, su desarrollo es una espiral de Arquímedes.

En el caso de una espiral hiperbólica ( ), el desarrollo es congruente con la espiral del plano del piso.${\displaystyle n=-1}$

En el caso de una espiral logarítmica, el desarrollo es una espiral logarítmica:${\displaystyle r=ae^{k\varphi }}$

${\displaystyle \rho =a{\sqrt {1+m^{2}}}\;e^{k{\sqrt {1+m^{2}}}\psi }\ .}$

Traza tangente

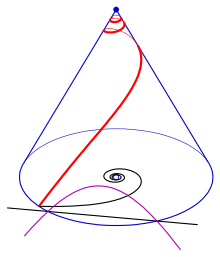
La traza (violeta) de las tangentes de una espiral cónica con una espiral hiperbólica como planta. La línea negra es la asíntota de la espiral hiperbólica.

La colección de puntos de intersección de las tangentes de una espiral cónica con el plano - (plano a través del vértice del cono) se denomina trazo tangente .${\displaystyle x}$${\displaystyle y}$

Para la espiral cónica

${\displaystyle (r\cos \varphi ,r\sin \varphi ,mr)}$

el vector tangente es

${\displaystyle (r'\cos \varphi -r\sin \varphi ,r'\sin \varphi +r\cos \varphi ,mr')^{T}}$

y la tangente:

${\displaystyle x(t)=r\cos \varphi +t(r'\cos \varphi -r\sin \varphi )\ ,}$

${\displaystyle y(t)=r\sin \varphi +t(r'\sin \varphi +r\cos \varphi )\ ,}$

${\displaystyle z(t)=mr+tmr'\ .}$

El punto de intersección con el plano - tiene parámetro y el punto de intersección es${\displaystyle x}$${\displaystyle y}$${\displaystyle t=-r/r'}$

• ${\displaystyle \left({\frac {r^{2}}{r'}}\sin \varphi ,-{\frac {r^{2}}{r'}}\cos \varphi ,0\right)\ .}$

${\displaystyle r=a\varphi ^{n}}$da y la traza tangente es una espiral. En el caso (espiral hiperbólica) la traza tangente degenera en un círculo con radio (ver diagrama). Porque uno tiene y la traza tangente es una espiral logarítmica, que es congruente con el plano del piso, debido a la auto-semejanza de una espiral logarítmica.${\displaystyle \ {\tfrac {r^{2}}{r'}}={\tfrac {a}{n}}\varphi ^{n+1}\ }$${\displaystyle n=-1}$${\displaystyle a}$${\displaystyle r=ae^{k\varphi }}$${\displaystyle \ {\tfrac {r^{2}}{r'}}={\tfrac {r}{k}}\ }$

Conchas de caracol ( Neptunea angulata izquierda, derecha: Neptunea despecta

Referencias

1. Nuevo científico
2. Concospirales en el vuelo de los insectos
3. John D. Dyson: La antena espiral equiangular. En: Transacciones IRE sobre antenas y propagación. Vol. 7, 1959, págs. 181-187.
4. TA Kozlovskaya: La Concho-espiral en el cono. Vestn. Novosib. Gos. Univ., Ser. Estera. Mekh. Inform., 11: 2 (2011), págs. 65–76.
5. Siegmund Günther, Anton Edler von Braunmühl, Heinrich Wieleitner: Geschichte der Mathik . GJ Göschen, 1921, pág. 92.
6. Theodor Schmid: Darstellende Geometrie. Band 2, Vereinigung wissenschaftlichen Verleger, 1921, pág. 229.

enlaces externos

• Jamnitzer -Galerie: 3D-Spiralen. .
• Weisstein, Eric W. "Espiral cónica" . MathWorld .