Módulo plano

Estructura algebraica en la teoría de anillos

En álgebra , un módulo plano sobre un anillo R es un módulo R - M tal que tomar el producto tensorial sobre R con M conserva secuencias exactas . Un módulo es fielmente plano si tomar el producto tensorial con una secuencia produce una secuencia exacta si y solo si la secuencia original es exacta.

La planitud fue introducida por Jean-Pierre Serre  ( 1956 ) en su artículo Géometrie Algébrique et Géométrie Analytique . Véase también morfismo plano .

Definición

Un módulo M sobre un anillo R es plano si se cumple la siguiente condición: para cada mapa lineal inyectivo ${\displaystyle \varphi :K\to L}$de módulos R , el mapa

${\displaystyle \varphi \otimes _{R}M:K\otimes _{R}M\to L\otimes _{R}M}$

también es inyectivo, donde ${\displaystyle \varphi \otimes _{R}M}$ es el mapa inducido por ${\displaystyle k\otimes m\mapsto \varphi (k)\otimes m.}$

Para esta definición, basta con restringir las inyecciones. ${\displaystyle \varphi }$a las inclusiones de ideales finitamente generados en R .

De manera equivalente, un módulo R M es plano si el producto tensorial con M es un funtor exacto ; es decir, si, para cada breve secuencia exacta de módulos R${\displaystyle 0\rightarrow K\rightarrow L\rightarrow J\rightarrow 0,}$ la secuencia ${\displaystyle 0\rightarrow K\otimes _{R}M\rightarrow L\otimes _{R}M\rightarrow J\otimes _{R}M\rightarrow 0}$también es exacta. (Esta es una definición equivalente ya que el producto del tensor es un funtor exacto derecho ).

Estas definiciones se aplican también si R es un anillo no conmutativo y M es un módulo R izquierdo ; en este caso, K , L y J deben ser módulos R rectos, y los productos tensoriales no son módulos R en general, sino solo grupos abelianos .

Caracterizaciones

Planitud también se puede caracterizar por la siguiente condición ecuacional, lo que significa que R - relaciones lineal en M se derivan de las relaciones lineales en R . Un módulo R M es plano si y solo si, para cada relación lineal

${\displaystyle \sum _{i=1}^{m}r_{i}x_{i}=0}$

con ${\displaystyle r_{i}\in R}$ y ${\displaystyle x_{i}\in M}$, existen elementos ${\displaystyle y_{j}\in M}$ y ${\displaystyle a_{i,j}\in R,}$tal que ^[1]

${\displaystyle \sum _{i=1}^{m}r_{i}a_{i,j}=0\qquad {\text{and}}\qquad x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j}\quad {\text{for}}\quad i=1,\ldots ,n.}$

Es equivalente a definir n elementos de un módulo, y un mapa lineal de${\displaystyle R^{n}}$ a este módulo, que mapea la base estándar de ${\displaystyle R^{n}}$a los n elementos. Esto permite reescribir la caracterización anterior en términos de homomorfismos, de la siguiente manera.

Un módulo R M es plano si y solo si se cumple la siguiente condición: para cada mapa${\displaystyle f:F\to M,}$ donde ${\displaystyle F}$es un libre generado finitamente R -módulo, y por cada tipo finito R -submodule${\displaystyle K}$ de ${\displaystyle \ker f,}$ el mapa ${\displaystyle f}$factores a través de un mapa g a un módulo R libre${\displaystyle G}$ tal que ${\displaystyle g(K)=0:}$

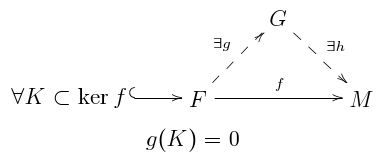
Relaciones con otras propiedades del módulo

La planitud está relacionada con varias otras propiedades del módulo, como ser libre, proyectivo o libre de torsión. En particular, cada módulo plano está libre de torsión , cada módulo proyectivo es plano y cada módulo libre es proyectivo.

Hay módulos finamente generados que son planos y no proyectivos. Sin embargo, todos los módulos generados de forma finita son proyectivos sobre los anillos que se consideran más comúnmente.

Esto se resume en parte en el siguiente gráfico.

Módulos sin torsión

Todos los módulos planos están libres de torsión . Esto resulta de la caracterización anterior en términos de relaciones tomando m = 1

Lo contrario se aplica a los números enteros y, de manera más general, a los principales dominios ideales y anillos de Dedekind .

Un dominio integral en el que cada módulo libre de torsión es plano se denomina dominio Prüfer .

Módulos libres y proyectivos

Un módulo M es proyectivo si y solo si hay un módulo G libre y dos mapas lineales${\displaystyle i:M\to G}$ y ${\displaystyle p:G\to M}$ tal que ${\displaystyle p\circ i=\mathrm {id} _{M}.}$ En particular, cada módulo gratuito es proyectivo (tome ${\displaystyle G=M}$ y ${\displaystyle i=p=\mathrm {id} _{M}}$).

Cada módulo proyectivo es plano. Esto se puede probar a partir de las caracterizaciones anteriores de planitud y proyectividad en términos de mapas lineales tomando${\displaystyle g=i\circ f}$ y ${\displaystyle h=p.}$

Por el contrario, los módulos planos generados de forma finita son proyectivos en condiciones suaves que generalmente se satisfacen en álgebra conmutativa y geometría algebraica . Esto hace que el concepto de planitud sea útil principalmente para módulos que no se generan de forma finita.

Un módulo presentado de forma finita (es decir, el cociente de un módulo libre generado de forma finita por un submódulo generado de forma finita) que es plano siempre es proyectivo. Esto se puede probar tomando f sobreyectiva y${\displaystyle K=\ker f}$en la caracterización anterior de la planitud en términos de mapas lineales. La condición${\displaystyle g(K)=0}$ implica la existencia de un mapa lineal ${\displaystyle i:M\to G}$ tal que ${\displaystyle i\circ f=g,}$ y por lo tanto ${\displaystyle h\circ i\circ f=h\circ g=f.}$Como f es sobreyectiva, uno tiene${\displaystyle h\circ i=\mathrm {id} _{M},}$y M es proyectiva.

Sobre un anillo noetheriano , cada módulo plano finamente generado es proyectivo, ya que cada módulo finitamente generado se presenta de forma finita. El mismo resultado es cierto sobre un dominio integral , incluso si no es noetheriano. ^[2]

En un anillo local, cada módulo plano generado de forma finita es gratuito.

Un módulo plano finamente generado que no es proyectivo se puede construir de la siguiente manera. Dejar${\displaystyle R=F^{\mathbb {N} }}$el conjunto de las secuencias infinitas cuyos términos pertenecen a un campo fijo F . Es un anillo conmutativo con la suma y la multiplicación definidas por componentes. Este anillo es absolutamente plano (es decir, todos los módulos son planos). El módulo${\displaystyle R/I,}$donde I es el ideal de las secuencias con un número finito de términos distintos de cero, es por tanto plano y finitamente generado (solo un generador), pero no es proyectivo.

No ejemplos

• Si I es un ideal en un anillo conmutativo noetheriano R , entonces${\displaystyle R/I}$no es un módulo plano, excepto si I es generado por un idempotente (que es un elemento igual a su cuadrado). En particular, si R es un dominio integral ,${\displaystyle R/I}$ es plano solo si ${\displaystyle I}$es igual a R o es el ideal cero .

• En un dominio integral, un módulo plano está libre de torsión . Por tanto, un módulo que contiene elementos de torsión distintos de cero no es plano. En particular${\displaystyle \mathbb {Q} /\mathbb {Z} }$ y todos los campos de características positivas no son planos ${\displaystyle \mathbb {Z} }$-módulos, donde ${\displaystyle \mathbb {Z} }$ es el anillo de números enteros, y ${\displaystyle \mathbb {Q} }$ es el campo de los números racionales.

Sumas, límites y productos directos

Una suma directa ${\displaystyle \textstyle \bigoplus _{i\in I}M_{i}}$ de módulos es plano y solo si cada ${\displaystyle M_{i}}$ es plano.

Un límite directo de plano es plano. En particular, un límite directo de módulos libres es plano. A la inversa, cada módulo plano se puede escribir como un límite directo de módulos libres generados de forma finita . ^[3]

En general, los productos directos de módulos planos no necesitan ser planos. De hecho, dado un anillo R , todo producto directo de módulos R planos es plano si y solo si R es un anillo coherente (es decir, cada ideal generado de forma finita se presenta de forma finita). ^[4]

Extensiones de anillo plano

Un homomorfismo de anillo ${\displaystyle R\to S}$es plano si S es un módulo R plano para la estructura del módulo inducida por el homomorfismo. Por ejemplo, el anillo de polinomios R [ t ] es plana sobre R , para cualquier anillo R .

Para cualquier subconjunto multiplicativo ${\displaystyle S}$ de un anillo conmutativo ${\displaystyle R}$, el anillo de localización ${\displaystyle S^{-1}R}$es plano sobre R (es proyectivo solo en casos excepcionales). Por ejemplo,${\displaystyle \mathbb {Q} }$ es plano y no proyectivo sobre ${\displaystyle \mathbb {Z} .}$

Si ${\displaystyle I}$es un ideal de un anillo conmutativo noetheriano${\displaystyle R,}$la terminación ${\displaystyle {\widehat {R}}}$ de ${\displaystyle R}$ con respecto a ${\displaystyle I}$es plano. ^[5] Es fielmente plano si y solo si${\displaystyle I}$está contenido en el radical Jacobson de${\displaystyle A.}$(Ver también anillo de Zariski .) ^[6]

Localización

En esta sección, R denota un anillo conmutativo . Si${\displaystyle {\mathfrak {p}}}$es un ideal primo de R , la localización en${\displaystyle {\mathfrak {p}}}$ es, como de costumbre, denotado con ${\displaystyle {\mathfrak {p}}}$como índice. Eso es,${\displaystyle R_{\mathfrak {p}}=S^{-1}R,}$y, si M es un módulo R ,${\displaystyle M_{\mathfrak {p}}=S^{-1}M=R_{\mathfrak {p}}\otimes _{R}M.}$

Si un módulo R M es plano, entonces${\displaystyle M_{\mathfrak {p}}}$ es un piso ${\displaystyle R_{\mathfrak {p}}}$-módulo para cada ideal principal ${\displaystyle {\mathfrak {p}}.}$

Por el contrario, si ${\displaystyle M_{\mathfrak {m}}}$ es un piso ${\displaystyle R_{\mathfrak {m}}}$-módulo para cada ideal máximo ${\displaystyle {\mathfrak {m}}}$, entonces M es un módulo R plano (y${\displaystyle M_{\mathfrak {p}}}$ es un piso ${\displaystyle R_{\mathfrak {p}}}$-módulo para cada ideal principal ${\displaystyle {\mathfrak {p}}}$).

Estas propiedades son fundamentales en el álgebra conmutativa, ya que reducen la cuestión de la planitud al caso de los anillos locales . A menudo se expresan diciendo que la llanura es una propiedad local .

Morfismos planos de esquemas

Un morfismo ${\displaystyle f:X\to Y}$de esquemas es un morfismo plano si el mapa inducido en anillos locales

${\displaystyle {\mathcal {O}}_{Y,f(x)}\to {\mathcal {O}}_{X,x}}$

es un homomorfismo anillo plano para cualquier punto x en X . Así, las propiedades de los homomorfismos de anillo planos (o fielmente planos) se extienden naturalmente a las propiedades geométricas de los morfismos planos en geometría algebraica. Por ejemplo, considere el ejemplo anterior de${\displaystyle R=\mathbb {C} [t,x,y]/(xy-t)}$. La inclusión${\displaystyle \mathbb {C} [t]\hookrightarrow R}$ luego determina el morfismo plano

${\displaystyle \pi :\operatorname {Spec} (R)\to \operatorname {Spec} (\mathbb {C} [t]).}$

Cada fibra (geométrica) ${\displaystyle \pi ^{-1}(t)}$ es la curva de la ecuación ${\displaystyle xy=t.}$Ver también degeneración plana y deformación a cono normal .

Dejar ${\displaystyle S=R[x_{1},\dots ,x_{r}]}$ ser un anillo polinomial sobre un anillo noetheriano conmutativo ${\displaystyle R}$ y ${\displaystyle f\in S}$un no zeodivisor. Luego${\displaystyle S/fS}$ es plano sobre ${\displaystyle R}$ si y solo si ${\displaystyle f}$es primitivo (los coeficientes generan la unidad ideal). ^[7] Un ejemplo es ^{[8] pág. 3} ${\displaystyle \mathbb {C} [t,x,y]/(xy-t),}$ que es plano (e incluso gratis) sobre ${\displaystyle \mathbb {C} [t]}$(ver también a continuación el significado geométrico). Estas extensiones planas se pueden utilizar para producir ejemplos de módulos planos que no son gratuitos y no son el resultado de una localización.

Llanura fiel

Un módulo es fielmente plano si, tomando el producto tensorial con una secuencia, se produce una secuencia exacta si y solo si la secuencia original es exacta. Aunque el concepto se define para módulos sobre un anillo conmutativo no necesario, se utiliza principalmente para álgebras conmutativas . Entonces, este es solo este caso que se considera aquí, incluso si algunos resultados pueden generalizarse al caso de módulos sobre un anillo no conmutativo.

En esta sección, ${\displaystyle f\colon R\to S}$es un homomorfismo de anillos conmutativos, que da a${\displaystyle S}$ las estructuras de un ${\displaystyle R}$-álgebra y un ${\displaystyle R}$-módulo. Si${\displaystyle S}$ es un ${\displaystyle R}$-módulo plano (o fielmente plano), se dice comúnmente que ${\displaystyle S}$ es plano (o fielmente plano) sobre ${\displaystyle R,}$ y eso ${\displaystyle f}$ es plano (o fielmente plano).

Si ${\displaystyle S}$ es plano sobre ${\displaystyle R,}$ Las siguientes condiciones son equivalentes.

• ${\displaystyle S}$ es fielmente plano.
• Por cada ideal máximo ${\displaystyle {\mathfrak {m}}}$ de ${\displaystyle R}$, uno tiene ${\displaystyle {\mathfrak {m}}S\neq S.}$
• Si ${\displaystyle M}$ es distinto de cero ${\displaystyle R}$-módulo, luego ${\displaystyle M\otimes _{R}S\neq 0.}$
• Por cada ideal principal ${\displaystyle {\mathfrak {p}}}$ de ${\displaystyle R,}$ hay un ideal primordial ${\displaystyle {\mathfrak {P}}}$ de ${\displaystyle S}$ tal que ${\displaystyle {\mathfrak {p}}=f^{-1}({\mathfrak {P}}).}$ En otras palabras, el mapa ${\displaystyle f^{*}\colon \operatorname {Spec} (S)\to \operatorname {Spec} (R)}$ Inducido por ${\displaystyle f}$en los espectros es sobreyectiva.
• ${\displaystyle f,}$ es inyectable, y ${\displaystyle R}$es un subanillo puro de${\displaystyle S;}$ eso es, ${\displaystyle M\to M\otimes _{R}S}$ es inyectable para cada ${\displaystyle R}$-módulo ${\displaystyle M}$. ^[9]

La segunda condición implica que un homomorfismo plano de anillos locales es fielmente plano. De la última condición se desprende que${\displaystyle I=IS\cap R}$ para cada ideal ${\displaystyle I}$ de ${\displaystyle R}$ (llevar ${\displaystyle M=R/I}$). En particular, si${\displaystyle S}$ es un anillo noetheriano, entonces ${\displaystyle R}$ también es noetheriano.

La última condición, excepto una, se puede establecer en la siguiente forma reforzada: ${\displaystyle \operatorname {Spec} (S)\to \operatorname {Spec} (R)}$es sumergible , lo que significa que la topología de Zariski de${\displaystyle \operatorname {Spec} (R)}$es la topología cociente de la de${\displaystyle \operatorname {Spec} (S)}$(Este es un caso especial del hecho de que un morfismo de esquemas cuasi-compacto fielmente plano tiene esta propiedad. ^[10] ). Véase también Morfismo plano # Propiedades de morfismos planos .

Ejemplos

• Un homomorfismo de anillo ${\displaystyle R\to S}$ tal que ${\displaystyle S}$es un módulo R libre distinto de cero es fielmente plano. Por ejemplo:
  • Cada extensión de campo es fielmente plana. Esta propiedad está implícitamente detrás del uso de la complexificación para probar resultados en espacios vectoriales reales.
  • Un anillo polinomial es una extensión fielmente plana de su anillo de coeficientes.
  • Si ${\displaystyle p\in R[x]}$es un polinomio monico , la inclusión${\displaystyle R\hookrightarrow R[t]/\langle f\rangle }$ es fielmente plano.
• Dejar ${\displaystyle t_{1},\ldots ,t_{k}\in R.}$El producto directo ${\displaystyle \textstyle \prod _{i}R[t_{i}^{-1}]}$de las localizaciones en el${\displaystyle t_{i}}$ es fielmente plano ${\displaystyle R}$ si y solo si ${\displaystyle t_{1},\ldots ,t_{k}}$generar la unidad ideal de${\displaystyle R}$ (es decir, si ${\displaystyle 1}$es una combinación lineal de la${\displaystyle t_{i}}$). ^[11]
• La suma directa de las localizaciones${\displaystyle R_{\mathfrak {p}}}$ de ${\displaystyle R}$ en todos sus ideales primarios es un módulo fielmente plano que no es un álgebra, excepto si hay un número finito de ideales primarios.

Los dos últimos ejemplos están implícitamente detrás del amplio uso de la localización en álgebra conmutativa y geometría algebraica.

• Para un homomorfismo de anillo dado ${\displaystyle f:A\to B,}$hay un complejo asociado llamado complejo Amitsur : ^[12]
  $${\displaystyle 0\to A{\overset {f}{\to }}B{\overset {\delta ^{0}}{\to }}B\otimes _{A}B{\overset {\delta ^{1}}{\to }}B\otimes _{A}B\otimes _{A}B\to \cdots }$$
  donde los operadores co-fronterizos ${\displaystyle \delta ^{n}}$son las sumas alternas de los mapas que se obtienen insertando 1 en cada lugar; p.ej,${\displaystyle \delta ^{0}(b)=b\otimes 1-1\otimes b}$. Entonces (Grothendieck) este complejo es exacto si${\displaystyle f}$ es fielmente plano.

Homomorfismos locales fielmente planos

Aquí hay una caracterización de un homomorfismo fielmente plano para un homomorfismo no necesariamente plano. Dado un homomorfismo local inyectivo${\displaystyle (R,{\mathfrak {m}})\hookrightarrow (S,{\mathfrak {n}})}$ tal que ${\displaystyle {\mathfrak {m}}S}$ es un ${\displaystyle {\mathfrak {n}}}$- ideal primario , el homomorfismo${\displaystyle S\to B}$es fielmente plano si y solo si el teorema de la transición es válido para él; es decir, para cada${\displaystyle {\mathfrak {m}}}$-ideal primario ${\displaystyle {\mathfrak {q}}}$ de ${\displaystyle R}$, ${\displaystyle \operatorname {length} _{S}(S/{\mathfrak {q}}S)=\operatorname {length} _{S}(S/{\mathfrak {m}}S)\operatorname {length} _{R}(R/{\mathfrak {q}}).}$^[13]

Caracterización homológica usando functores Tor

La planitud también se puede expresar utilizando los functores Tor , los functores derivados de la izquierda del producto tensorial. Un módulo R izquierdo M es plano si y solo si

${\displaystyle \operatorname {Tor} _{n}^{R}(X,M)=0}$ para todos ${\displaystyle n\geq 1}$y bien R -módulos X ). ^[14]

De hecho, basta con comprobar que el primer término Tor desaparece, es decir, M es plano si y solo si

${\displaystyle \operatorname {Tor} _{1}^{R}(N,M)=0}$

para cualquier R -módulo N o, incluso más restrictivamente, cuando${\displaystyle N=R/I}$ y ${\displaystyle I\subset R}$ es cualquier ideal finitamente generado.

Usando las largas secuencias exactas del functor Tor , uno puede probar fácilmente hechos sobre una secuencia corta exacta

${\displaystyle 0\to A{\overset {f}{\longrightarrow }}B{\overset {g}{\longrightarrow }}C\to 0}$

Si A y C son planas, entonces también lo es B . También, si B y C son planas, entonces también lo es A . Si A y B son planos, C no necesita ser plano en general. Sin embargo, si A es puro en B y B es plano, entonces A y C son planos.

Resoluciones planas

Una resolución plana de un módulo M es una resolución de la forma

${\displaystyle \cdots \to F_{2}\to F_{1}\to F_{0}\to M\to 0,}$

donde F _i son todos módulos planos. Cualquier resolución libre o proyectiva es necesariamente una resolución plana. Se pueden usar resoluciones planas para calcular el functor Tor .

La longitud de una resolución plana finita es el primer subíndice n tal que${\displaystyle F_{n}}$ es distinto de cero y ${\displaystyle F_{i}=0}$ por ${\displaystyle i>n}$. Si un módulo M admite una resolución plana finita, la longitud mínima entre todas las resoluciones planas finitas de M se denomina dimensión plana ^[15] y se denota fd ( M ). Si M no admite una resolución plana finita, entonces por convención se dice que la dimensión plana es infinita. Como ejemplo, considere un módulo M tal que fd ( M ) = 0. En esta situación, la exactitud de la secuencia 0 → F ₀ → M → 0 indica que la flecha en el centro es un isomorfismo y, por lo tanto, M en sí es plano. ^[dieciséis]

En algunas áreas de la teoría de módulos, una resolución plana debe satisfacer el requisito adicional de que cada mapa es una pre-cubierta plana del núcleo del mapa a la derecha. Para las resoluciones proyectivas, esta condición es casi invisible: una precubierta proyectiva es simplemente un epimorfismo de un módulo proyectivo. Estas ideas están inspiradas en el trabajo de Auslander en aproximaciones. Estas ideas también son familiares a partir de la noción más común de resoluciones proyectivas mínimas, donde se requiere que cada mapa sea una cubierta proyectiva del núcleo del mapa a la derecha. Sin embargo, las cubiertas proyectivas no necesitan existir en general, por lo que las resoluciones proyectivas mínimas solo tienen un uso limitado sobre anillos como los enteros.

Cubiertas planas

Si bien no siempre existen cubiertas proyectivas para módulos, se especuló que para los anillos generales, cada módulo tendría una cubierta plana, es decir, cada módulo M sería la imagen epimórfica de un módulo plano F de manera que cada mapa de un módulo plano sobre M factores a través de F , y cualquier endomorfismo de F sobre M es un automoprismo. Esta conjetura de la cubierta plana se enunció explícitamente por primera vez en ( Enochs 1981 , p 196) . La conjetura resultó ser cierta, resuelta positivamente y probada simultáneamente por L. Bican, R. El Bashir y E. Enochs. ^[17] harv error: no target: CITEREFEnochs1981 (help) Esto fue precedido por importantes contribuciones de P. Eklof, J. Trlifaj y J. Xu.

Dado que existen cubiertas planas para todos los módulos en todos los anillos, las resoluciones planas mínimas pueden reemplazar las resoluciones proyectivas mínimas en muchas circunstancias. La medida de la desviación de las resoluciones planas de las resoluciones proyectivas se llama álgebra homológica relativa y se trata en clásicos como ( MacLane 1963 ) y en trabajos más recientes que se centran en resoluciones planas como ( Enochs & Jenda 2000 ). harv error: no target: CITEREFMacLane1963 (help)

En matemáticas constructivas

Los módulos planos tienen una importancia creciente en las matemáticas constructivas , donde los módulos proyectivos son menos útiles. Por ejemplo, que todos los módulos libres sean proyectivos equivale al axioma completo de elección , por lo que los teoremas sobre módulos proyectivos, incluso si se prueban constructivamente, no se aplican necesariamente a los módulos libres. Por el contrario, no se necesita ninguna opción para demostrar que los módulos libres son planos, por lo que los teoremas sobre los módulos planos aún pueden aplicarse. ^[18]

Ver también

• Planitud genérica
• Morfismo plano
• Anillo regular de von Neumann : aquellos anillos sobre los que todos los módulos son planos.
• Anillo normalmente plano

Referencias

1. Bourbaki , cap. I, § 2. Proposición 13, Corolario 1.
2. Cartier, Pierre (1958). "Preguntas de racionalidad des diviseurs en géométrie algébrique" . Bulletin de la Société Mathématique de France (en francés). Déjame 5, página 249. 86 : 177-251. doi : 10.24033 / bsmf.1503 .
3. ( Lazard, 1969 )
4. ( Chase 1960 )
5. Matsumura 1970 , Corolario 1 del Teorema 55, p. 170
6. Matsumura 1970 , Teorema 56
7. Eisenbud , ejercicio 6.4. harvnb error: no target: CITEREFEisenbud (help)
8. Artin. "Teoría de la deformación" (PDF) . Archivado (PDF) desde el original el 28 de octubre de 2020.
9. Prueba: Supongamos${\displaystyle f:R\to S}$es fielmente plano. Para un módulo R${\displaystyle M,}$ el mapa ${\displaystyle S=R\otimes _{R}S\to S\otimes _{R}S}$ exhibiciones ${\displaystyle S}$ como un puro subring y así ${\displaystyle M\otimes _{R}S\to M\otimes _{R}(S\otimes S)\simeq (M\otimes _{R}S)\otimes _{R}S}$es inyectable. Por eso,${\displaystyle M\to M\otimes _{R}S}$es inyectable. Por el contrario, si${\displaystyle M\neq 0}$ es un módulo sobre ${\displaystyle R}$, luego ${\displaystyle 0\neq M\subset M\otimes _{R}S.}$
10. SGA 1 , Exposé VIII., Corollay 4.3. harvnb error: no target: CITEREFSGA_1 (help)
11. Artin , Ejercicio (3) después de la Proposición III.5.2.
12. "Complejo de Amitsur" . ncatlab.org .
13. Matsumura 1986 , cap. 8, ejercicio 22.1.
14. De manera similar, unmódulo R derecho M es plano si y solo si${\displaystyle \operatorname {Tor} _{n}^{R}(M,X)=0}$ para todos ${\displaystyle n\geq 1}$y todos izquierda R -modules X .
15. Lam 1999 , p. 183.
16. Un módulo isomorfo a un módulo plano es, por supuesto, plano.
17. Bican, El Bashir y Enochs 2001 .
18. Richman 1997 .

• Artin, Michael (1999). "Anillos no conmutativos" (PDF) .
• Bican, L .; El Bashir, R .; Enochs, E. (2001), "Todos los módulos tienen cubiertas planas", Bull. London Math. Soc. , 33 (4): 385–390, doi : 10.1017 / S0024609301008104 , ISSN  0024-6093 , MR  1832549
• Bourbaki, Nicolas . Álgebra conmutativa .
• Chase, Stephen U. (1960), "Direct products of modules", Transactions of the American Mathematical Society , 97 (3): 457–473, doi : 10.2307 / 1993382 , JSTOR  1993382 , MR  0120260
• Eisenbud, David (1995), álgebra conmutativa , Textos de posgrado en matemáticas , 150 , Berlín, Nueva York: Springer-Verlag , doi : 10.1007 / 978-1-4612-5350-1 , ISBN 978-0-387-94268-1, MR  1322960
• Enochs, Edgar E. (1981), "Cubiertas, sobres y solventes inyectables y planos", Israel Journal of Mathematics , 39 (3): 189–209, doi : 10.1007 / BF02760849 , ISSN  0021-2172 , MR  0636889 , S2CID  120567780
• Enochs, Edgar E .; Jenda, Overtoun MG (2000), Álgebra homológica relativa , Exposiciones de Gruyter en matemáticas, 30 , Berlín: Walter de Gruyter & Co., doi : 10.1515 / 9783110803662 , ISBN 978-3-11-016633-0, Señor  1753146
• Kunz, Ernst (1969), "Caracterizaciones de anillos locales regulares de característica p ", American Journal of Mathematics , 91 (3): 772–784, doi : 10.2307 / 2373351 , JSTOR  2373351 , MR  0252389
• Lam, Tsit-Yuen (1999), Conferencias sobre módulos y anillos , Textos de posgrado en matemáticas No. 189, 189 , Berlín, Nueva York: Springer-Verlag , doi : 10.1007 / 978-1-4612-0525-8 , ISBN 978-0-387-98428-5, MR  1653294
• Lazard, Daniel (1969), "Autour de la platitude" , Bulletin de la Société Mathématique de France , 97 : 81–128, doi : 10.24033 / bsmf.1675
• Mac Lane, Saunders (1963), Homología , Die Grundlehren der mathischen Wissenschaften, Bd. 114, Boston, MA: Academic Press , MR  0156879
• Matsumura, Hideyuki (1970), álgebra conmutativa
• Matsumura, Hideyuki (1986). Teoría del anillo conmutativo . Estudios de Cambridge en Matemáticas Avanzadas. 8 . Prensa de la Universidad de Cambridge. ISBN 0-521-36764-6. Señor  0879273 . Zbl  0603.13001 .
• Mumford, David , El libro rojo de variedades y esquemas
• Northcott, DG (1984), álgebra multilineal , Cambridge University Press , ISBN 978-0-521-26269-9 - página 33
• Richman, Fred (1997), "Dimensión plana, constructividad y el teorema de la sicigia de Hilbert", New Zealand Journal of Mathematics , 26 (2): 263-273, ISSN  1171-6096 , MR  1601663
• Serre, Jean-Pierre (1956), "Géométrie algébrique et géométrie analytique" , Annales de l'Institut Fourier , 6 : 1–42, doi : 10.5802 / aif.59 , ISSN  0373-0956 , MR  0082175