De Wikipedia, la enciclopedia libre
Ir a navegaciónSaltar a buscar

En la teoría de grupos , una rama de las matemáticas, el teorema de Nielsen-Schreier establece que cada subgrupo de un grupo libre es en sí mismo libre. [1] [2] [3] Lleva el nombre de Jakob Nielsen y Otto Schreier .

Declaración del teorema

Un grupo libre puede definirse a partir de una presentación de grupo que consta de un conjunto de generadores sin relaciones. Es decir, cada elemento es un producto de alguna secuencia de generadores y sus inversas, pero estos elementos no obedecen a ninguna ecuación excepto a las que se siguen trivialmente de gg −1 = 1. Los elementos de un grupo libre pueden describirse como todas las posibles palabras reducidas. , esas cadenas de generadores y sus inversos en los que ningún generador es adyacente a su propio inverso. Se pueden multiplicar dos palabras reducidas concatenandolas y luego eliminando cualquier par generador-inverso que resulte de la concatenación.

El teorema de Nielsen-Schreier establece que si H es un subgrupo de un grupo libre G , entonces H es en sí mismo isomorfo a un grupo libre. Esto es, existe un conjunto S de elementos que generan H , sin relaciones no triviales entre los elementos de S .

La fórmula de Nielsen-Schreier , o fórmula del índice de Schreier , cuantifica el resultado en el caso en que el subgrupo tiene un índice finito: si G es un grupo libre de rango n (libre en n generadores), y H es un subgrupo de índice finito [ G  : H ] = e , entonces H está libre de rango. [4]

Ejemplo

Sea G el grupo libre con dos generadores, y sea H el subgrupo que consiste en todas las palabras reducidas de longitud par (productos de un número par de letras). Entonces H es generado por sus seis elementosUna factorización de cualquier palabra reducida en H en estos generadores y sus inversas puede construirse simplemente tomando pares consecutivos de letras en la palabra reducida. Sin embargo, esta no es una presentación gratuita de H porque los tres últimos generadores se pueden escribir en términos de los tres primeros como. Más bien, H se genera como un grupo libre por los tres elementosque no tienen relaciones entre ellos; o en su lugar por varios otros triples de los seis generadores. [5] Además, G está libre en n = 2 generadores, H tiene índice e = [ G  : H ] = 2 en G , y H está libre en 1 + e ( n –1) = 3 generadores. El teorema de Nielsen-Schreier establece que, como H , cada subgrupo de un grupo libre se puede generar como un grupo libre, y si el índice de H es finito, su rango viene dado por la fórmula del índice.

Prueba

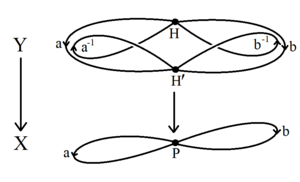
El grupo libre G = π 1 ( X ) tiene n = 2 generadores correspondientes a bucles de un , b desde el punto base P en X . El subgrupo H de palabras pares, con índice e = [ G  : H ] = 2, corresponde al gráfico de cobertura Y con dos vértices correspondientes a las clases laterales H y H ' = aH = bH = a −1 H = b - 1 horay dos bordes elevados para cada uno de los bordes de bucle originales a , b . Contraer uno de los bordes de Y da una equivalencia de homotopía a un ramo de tres círculos, de modo que H = π 1 ( Y ) es un grupo libre en tres generadores, por ejemplo aa , ab , ba .

Una breve demostración del teorema de Nielsen-Schreier utiliza la topología algebraica de grupos fundamentales y espacios de cobertura . [1] Un grupo libre G en un conjunto de generadores es el grupo fundamental de un ramo de círculos , un gráfico topológico X con un solo vértice y con un borde de bucle para cada generador. [6] Cualquier subgrupo H del grupo fundamental es en sí mismo el grupo fundamental de un espacio de cobertura conectado Y → X. El espacio Y es un gráfico topológico (posiblemente infinito), el gráfico de clase lateral de Schreierque tiene un vértice para cada clase lateral en G / H . [7] En cualquier gráfico topológico conectado, es posible reducir el tamaño de los bordes de un árbol de expansión de la gráfica, la producción de un ramo de círculos que tiene el mismo grupo fundamental H . Dado que H es el grupo fundamental de un ramo de círculos, él mismo es libre. [6]

La homología simple permite calcular el rango de H , que es igual ah 1 ( Y ), el primer número Betti del espacio de cobertura, el número de ciclos independientes. Para G sin rango n , el gráfico X tiene n aristas y 1 vértice; suponiendo que H tiene un índice finito [ G  : H ] = e , el gráfico de cobertura Y tiene bordes en yevértices. El primer número Betti de un gráfico es igual al número de aristas, menos el número de vértices, más el número de componentes conectados; por tanto, el rango de H es:

Esta prueba se debe a Reinhold Baer y Friedrich Levi  ( 1936 ); la prueba original por Schreier forma el gráfico Schreier de una manera diferente como un cociente de la gráfica Cayley de G modulo la acción de H . [8]

De acuerdo con el lema del subgrupo de Schreier, se puede construir un conjunto de generadores para una presentación libre de H a partir de ciclos en el gráfico de cobertura formado mediante la concatenación de una trayectoria de árbol de expansión desde un punto base (la clase lateral de la identidad) a una de las clases laterales, una borde único que no es de árbol y una ruta de árbol de expansión inversa desde el otro punto final del borde hasta el punto base. [9] [8]

Fundamentos axiomáticos

Aunque se conocen varias demostraciones diferentes del teorema de Nielsen-Schreier, todas dependen del axioma de elección . En la demostración basada en grupos fundamentales de ramos, por ejemplo, el axioma de elección aparece bajo la apariencia de la afirmación de que todo gráfico conectado tiene un árbol de expansión. El uso de este axioma es necesario, ya que existen modelos de teoría de conjuntos de Zermelo-Fraenkel en los que el axioma de elección y el teorema de Nielsen-Schreier son falsos. El teorema de Nielsen-Schreier, a su vez, implica una versión más débil del axioma de elección, para conjuntos finitos. [10] [11]

Historia

El teorema de Nielsen-Schreier es un análogo no abeliano de un resultado anterior de Richard Dedekind , que cada subgrupo de un grupo abeliano libre es abeliano libre . [3]

Jakob Nielsen ( 1921 ) demostró originalmente una forma restringida del teorema, afirmando que cualquier subgrupo generado de forma finita de un grupo libre es libre. Su demostración consiste en realizar una secuencia de transformaciones de Nielsen en el grupo electrógeno del subgrupo que reducen su longitud (como palabras reducidas en el grupo libre del que se extraen). [1] [12] Otto Schreier demostró el teorema de Nielsen-Schreier en toda su generalidad en su tesis de habilitación de 1926 , Die Untergruppen der freien Gruppe , también publicada en 1927 en Abh. Matemáticas. Sem. Hamburgo. Univ. [13] [14]

La prueba topológica basada en grupos fundamentales de ramos de círculos se debe a Reinhold Baer y Friedrich Levi  ( 1936 ). Otra prueba topológica, basada en la teoría de Bass-Serre de acciones grupales sobre árboles , fue publicada por Jean-Pierre Serre  ( 1970 ). [15]

Ver también

  • Teorema fundamental de los grupos cíclicos , un resultado similar para los grupos cíclicos que en el caso infinito puede verse como un caso especial del teorema de Nielsen-Schreier

Notas

  1. ↑ a b c Stillwell (1993) , Sección 2.2.4, El teorema de Nielsen-Schreier, págs. 103-104.
  2. ^ Magnus, Karass y Solitar 1976 , Corolario 2.9, p. 95.
  3. ↑ a b Johnson (1980) , Sección 2, El teorema de Nielsen-Schreier, págs. 9-23.
  4. ^ Fried y Jarden (2008) , p. 355
  5. ^ Johnson (1997) , ej. 15, pág. 12.
  6. ↑ a b Stillwell (1993) , Sección 2.1.8, Freeness of the Generators, p. 97.
  7. ^ Stillwell (1993) , Sección 2.2.2, La propiedad del subgrupo, págs. 100-101.
  8. ↑ a b Bollobas, Bela (1998). "Capítulo VIII.1". Teoría de grafos moderna . Springer Verlag. pag. 262. ISBN 978-0-387-98488-9.
  9. ^ Stillwell (1993) , sección 2.2.6, Schreier Transversals, págs. 105-106.
  10. ↑ Läuchli (1962)
  11. ^ Howard (1985) .
  12. ^ Magnus, Karass & Solitar 1976 , Sección 3.2, Un proceso de reducción, págs. 121-140.
  13. ^ O'Connor, John J .; Robertson, Edmund F. , "Teorema de Nielsen-Schreier" , archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews Parámetro desconocido |name=ignorado ( ayuda )
  14. ^ Hansen, Vagn Lundsgaard (1986), Jakob Nielsen, Documentos matemáticos recopilados: 1913-1932 , Birkhäuser, p. 117, ISBN 978-0-8176-3140-6.
  15. ^ Rotman (1995) , El teorema de Nielsen-Schreier, págs. 383–387.

Referencias

  • Baer, ​​Reinhold ; Levi, Friedrich (1936), "Freie Produkte und ihre Untergruppen", Compositio Mathematica , 3 : 391–398.
  • Fried, Michael D .; Jarden, Moshe (2008), Aritmética de campo , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 11 (3ª ed.), Springer-Verlag , pág. 70, ISBN 978-3-540-77269-9, Zbl  1145.12001.
  • Howard, Paul E. (1985), "Subgrupos de un grupo libre y el axioma de elección", The Journal of Symbolic Logic , 50 (2): 458–467, doi : 10.2307 / 2274234 , JSTOR  2274234 , MR  0793126.
  • Johnson, DL (1980), Temas de la teoría de presentaciones grupales , serie de notas de conferencia de la London Mathematical Society, 42 , Cambridge University Press, ISBN 978-0-521-23108-4.
  • Johnson, DL (1997), Presentaciones de grupos , textos de estudiantes de la London Mathematical Society, 15 (2a ed.), Cambridge University Press, ISBN 978-0-521-58542-2.
  • Läuchli, Hans (1962), "Auswahlaxiom in der Algebra", Commentarii Mathematici Helvetici , 37 : 1–18, doi : 10.1007 / bf02566957 , hdl : 20.500.11850 / 131689 , MR  0143705 , S2CID  186223589.
  • Magnus, Wilhelm ; Karrass, Abraham; Solitar, Donald (1976), Teoría de grupos combinatorios (segunda edición revisada), Publicaciones de Dover.
  • Nielsen, Jakob (1921), "Om regning med ikke-kommutative faktorer og dens anvendelse i gruppeteorien", Math. Tidsskrift B (en danés), 1921 : 78–94, JFM  48.0123.03.
  • Rotman, Joseph J. (1995), Introducción a la teoría de grupos , Textos de posgrado en matemáticas, 148 (4a ed.), Springer-Verlag, ISBN 978-0-387-94285-8.
  • Serre, J.-P. (1970), Groupes Discretes , Extrait de I'Annuaire du College de France, París.
  • Serre, J.-P. (1980), Árboles , Springer-Verlag, ISBN 3-540-10103-9.
  • Stillwell, John (1993), Topología clásica y teoría combinatoria de grupos , Textos de posgrado en matemáticas, 72 (2a ed.), Springer-Verlag.