Prisma (geometría)

Forma geométrica, un poliedro con una base poligonal de n lados

Conjunto de prismas n -gonales uniformes
Ejemplo de prisma hexagonal uniforme
Escribe	uniforme en el sentido de poliedro semirregular
Notación de poliedro de Conway	P n
Caras	2 { n } + n {4}
Bordes	3 n
Vértices	2 n
Símbolo de Schläfli	{ n } × {} [1] o t {2,  n }
Diagrama de Coxeter
Configuración de vértice	4.4. norte
Grupo de simetría	D n h , [ n , 2], (* n 22), orden 4 n
Grupo de rotacion	D n , [ n , 2] + , ( n 22), orden 2 n
Poliedro doble	bipirámide convexa dual- uniforme n -gonal
Propiedades	convexas, caras de polígonos regulares , vértices transitivos , bases trasladadas, lados ⊥ bases [2]
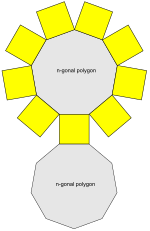Ejemplo de red de prisma enneagonal uniforme ( n = 9)

En geometría , un prisma es un poliedro que comprende un n -sided polígono de base , una segunda base que es un traducido copia (rígidamente movidos sin rotación) de la primera, y n otras caras , necesariamente todos los paralelogramos , uniéndose a los lados correspondientes de las dos bases . Todas las secciones transversales paralelas a las bases son traslaciones de las bases. Los prismas reciben el nombre de sus bases; ejemplo: un prisma con una base pentagonal se llama prisma pentagonal. Los prismas son una subclase de prismatoides .

Como muchos términos geométricos básicos, la palabra prisma ( griego : πρίσμα , romanizado :  prisma , literalmente  , 'algo aserrado') se utilizó por primera vez en los Elementos de Euclides . Euclides definió el término en el Libro XI como “una figura sólida contenida por dos planos opuestos, iguales y paralelos, mientras que el resto son paralelogramos”. Sin embargo, esta definición ha sido criticada por no ser lo suficientemente específica en relación con la naturaleza de las bases, lo que causó confusión entre los escritores de geometría posteriores. ^{[3] [4]}

Prisma oblicuo

Un prisma oblicuo es un prisma en el que los bordes y las caras de unión no son perpendiculares a las caras de la base.

Ejemplo: un paralelepípedo es un prisma oblicuo cuya base es un paralelogramo , o equivalentemente un poliedro con seis caras que son todas paralelogramos.

Prisma derecho, prisma uniforme

Prisma derecho

Un prisma recto es un prisma en el que los bordes y las caras de unión son perpendiculares a las caras de la base. ^[2] Esto se aplica si todas las caras de unión son rectangulares .

El doble de un derecho n -prism es un derecho n - bipirámide .

Un prisma recto (con lados rectangulares) con bases regulares de n- gones tiene el símbolo de Schläfli {} × { n }. Se aproxima a un sólido cilíndrico cuando n se acerca al infinito .

Casos especiales

• Un prisma rectangular recto (con una base rectangular) también se llama cuboide , o informalmente una caja rectangular . Un prisma rectangular recto tiene el símbolo de Schläfli {} × {} × {}.

• Un prisma cuadrado recto (con una base cuadrada) también se llama cuboide cuadrado , o informalmente caja cuadrada .

Nota: algunos textos pueden aplicar el término prisma rectangular o prisma cuadrado tanto a un prisma recto de base rectangular como a un prisma recto de base cuadrada.

Prisma uniforme

Un prisma uniforme o prisma semirregular es un prisma recto con bases regulares y lados cuadrados , ya que dichos prismas están en el conjunto de poliedros uniformes .

Un prisma n -gonal uniforme tiene el símbolo de Schläfli t {2, n }.

Los prismas rectos con bases regulares y longitudes de borde iguales forman una de las dos series infinitas de poliedros semirregulares , siendo la otra serie antiprismas .

Familia de prismas n -gonales uniformes

• v
• t
• mi

Nombre del prisma	Prisma digital	(Trigonal) Prisma triangular	(Tetragonal) Prisma cuadrado	Prisma pentagonal	Prisma hexagonal	Prisma heptagonal	Prisma octogonal	Prisma enneagonal	Prisma decagonal	Prisma hedecagonal	Prisma dodecagonal	...	Prisma apeirogonal
Imagen de poliedro												...
Imagen de mosaico esférico												Plane tiling image
Vertex config.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Volumen

El volumen de un prisma es el producto del área de la base y la distancia entre las dos caras de la base, o la altura (en el caso de un prisma no recto, tenga en cuenta que esto significa la distancia perpendicular).

Por tanto, el volumen es:

${\displaystyle V=Bh}$

donde B es el área de la base y h es la altura. Por lo tanto, el volumen de un prisma cuya base es un polígono regular de n lados con una longitud de lado s es:

${\displaystyle V={\frac {n}{4}}hs^{2}\cot \left({\frac {\pi }{n}}\right)}$

Superficie

El área de la superficie de un prisma recto es:

${\displaystyle 2B+Ph}$

donde B es el área de la base, h la altura y P el perímetro de la base .

El área de superficie de un prisma recto cuya base es un polígono regular de n lados con longitud de lado sy altura h es, por lo tanto:

${\displaystyle A={\frac {n}{2}}s^{2}\cot {\left({\frac {\pi }{n}}\right)}+nsh}$

Diagramas de Schlegel

P3

P4

P5

P6

P7

P8

Simetría

El grupo de simetría de un prisma de n lados rectos con base regular es D n h de orden 4 n , excepto en el caso de un cubo, que tiene el grupo de simetría más grande O h de orden 48, que tiene tres versiones de D _4h como subgrupos . El grupo de rotación es D _n de orden 2 n , excepto en el caso de un cubo, que tiene el grupo de simetría mayor O de orden 24, que tiene tres versiones de D ₄ como subgrupos.

El grupo de simetría D _{n h} contiene inversión si f n es par.

El hosoedro y el dihedra también poseen simetría diedro, y se puede construir un prisma n -gonal mediante el truncamiento geométrico de un hosoedro n -gonal, así como mediante la cantelación o expansión de un diedro n -gonal.

Prisma truncado

Un prisma truncado es un prisma con caras superior e inferior no paralelas . ^[5]

Ejemplo de prisma triangular truncado. Su cara superior está truncada en un ángulo oblicuo, ¡pero NO es un prisma oblicuo !

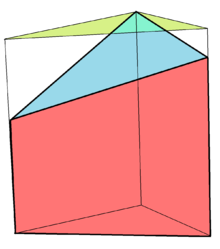
Prisma retorcido

Un prisma retorcido es un poliedro no convexo construido a partir de un prisma n uniforme con cada cara lateral dividida en dos en la diagonal cuadrada, girando la parte superior, generalmente porπ/norte radianes180/nortegrados) en la misma dirección, haciendo que los lados sean cóncavos. ^{[6] [7]}

Un prisma retorcido no se puede diseccionar en tetraedros sin agregar nuevos vértices. El caso más pequeño: la forma triangular, se llama poliedro de Schönhardt .

Un prisma retorcido n -gonal es topológicamente idéntico al antiprisma uniforme n -gonal , pero tiene la mitad del grupo de simetría : D _n , [ n , 2] ⁺ , orden 2 n . Puede verse como un antiprisma no convexo, con tetraedros eliminados entre pares de triángulos.

3-gonal	4-gonal		12 gonales
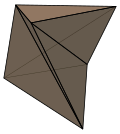Poliedro de Schönhardt	Prisma cuadrado retorcido	Antiprisma cuadrado	Antiprisma dodecagonal torcido

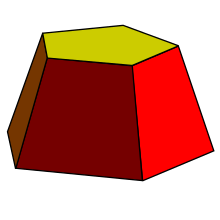
Frustum

Un tronco es una construcción similar a un prisma, con caras laterales trapezoidales y polígonos superior e inferior de diferentes tamaños.

Ejemplo tronco pentagonal

Prisma de estrella

Un prisma de estrella es un poliedro no convexo construido por dos caras de polígono de estrella idénticas en la parte superior e inferior, paralelas y desplazadas por una distancia y conectadas por caras rectangulares. Un prisma de estrella uniforme tendrá el símbolo de Schläfli { p / q } × {}, con p rectángulo y 2 { p / q } caras. Es topológicamente idéntico a un prisma p -gonal.

Ejemplos de

{} × {} 180 × {}	t a {3} × {}		{5/2} × {}	{7/2} × {}	{7/3} × {}	{8/3} × {}
D 2h , orden 8	D 3h , orden 12		D 5h , orden 20	D 7h , orden 28		D 8h , orden 32

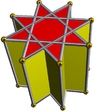Prisma cruzado

Un prisma cruzado es un poliedro no convexo construido a partir de un prisma, donde los vértices de una base se invierten alrededor del centro de esta base (o giran 180 °). Esto transforma las caras rectangulares laterales en rectángulos cruzados . Para una base de polígono regular, la apariencia es un n -gonal vidrio horas . Todos los bordes oblicuos pasan por un solo centro del cuerpo. Nota: ningún vértice está en este centro del cuerpo. Un prisma cruzado es topológicamente idéntico a un prisma n -gonal.

Ejemplos de

{} × {} 180 × {} 180	t a {3} × {} 180		{3} × {} 180	{4} × {} 180	{5} × {} 180	{5/2} × {} 180	{6} × {} 180
D 2h , orden 8	D 3d , orden 12			D 4h , orden 16	D 5d , orden 20		D 6d , orden 24

Prisma toroidal

Un prisma toroidal es un poliedro no convexo como un prisma cruzado , pero sin caras de base inferior y superior, y con caras laterales rectangulares simples que cierran el poliedro. Esto solo se puede hacer para polígonos base de lados pares. Estos son toros topológicos, con la característica de Euler de cero. La red poliédrica topológica se puede cortar a partir de dos filas de un mosaico cuadrado (con configuración de vértice 4.4.4.4 ): una banda de n cuadrados, cada uno unido a un rectángulo cruzado . Un prisma toroidal n -gonal tiene 2 n vértices, 2 n caras: n cuadrados yn rectángulos cruzados y 4 n aristas. Es topológicamente auto-dual .

Ejemplos de

D 4h , orden 16	D 6h , orden 24
v = 8, e = 16, f = 8	v = 12, e = 24, f = 12

Politopo prismático

Un politopo prismático es una generalización de mayor dimensión de un prisma. Un politopo prismático n -dimensional se construye a partir de dos ( n - 1 ) politopos dimensionales, traducidos a la siguiente dimensión.

Los elementos prismáticos n- politopos se duplican a partir de los elementos ( n - 1 ) -politopos y luego se crean nuevos elementos a partir del siguiente elemento inferior.

Tome un n -politopo con elementos f _i i -face ( i = 0, ..., n ). Su prisma de politopo ( n + 1 ) tendrá 2 elementos de cara f _i + f _{i −1} i . (Con f ₋₁ = 0 , f _n = 1. )

Por dimensión:

• Tome un polígono con n vértices, n aristas. Su prisma tiene 2 n vértices, 3 n aristas y 2 + n caras.
• Tome un poliedro con vértices v , aristas e y caras f . Su prisma tiene 2 vértices v , 2 aristas e + v , 2 caras f + e y 2 + f celdas.
• Tome un policorón con vértices v , aristas e , caras f y celdas c . Su prisma tiene 2 vértices v , 2 aristas e + v , 2 caras f + e , 2 celdas c + f y 2 hipercélulas + c .
  

Politopo prismático uniforme

Un politopo n regular representado por el símbolo de Schläfli { p , q , ...,  t } puede formar un politopo prismático uniforme ( n + 1 ) representado por un producto cartesiano de dos símbolos de Schläfli : { p , q , ... ,  t } × {}.

Por dimensión:

• Un prisma 0-politópico es un segmento de línea , representado por un símbolo de Schläfli vacío {}.
  • 
• Un prisma 1-politópico es un rectángulo , formado por 2 segmentos de línea trasladados. Se representa como el símbolo del producto Schläfli {} × {}. Si es cuadrado , la simetría se puede reducir: {} × {} = {4}.
  • Ejemplo: Cuadrado, {} × {}, dos segmentos de línea paralelos, conectados por dos lados de segmento de línea .
• Un prisma poligonal es un prisma tridimensional hecho de dos polígonos trasladados conectados por rectángulos. Un polígono regular { p } puede construir un prisma n -gonal uniforme representado por el producto { p } × {}. Si p = 4 , con simetría de lados cuadrados se convierte en un cubo : {4} × {} = {4, 3}.
  • Ejemplo: prisma pentagonal , {5} × {}, dos pentágonos paralelos conectados por 5 lados rectangulares .
• Un prisma poliédrico es un prisma de 4 dimensiones hecho de dos poliedros trasladados conectados por celdas de prisma de 3 dimensiones. Un poliedro regular { p ,  q } puede construir el prisma policórico uniforme, representado por el producto { p ,  q } × {}. Si el poliedro es un cubo y los lados son cubos, se convierte en un tesseract : {4, 3} × {} = {4, 3, 3}.
  • Ejemplo: prisma dodecaédrico , {5, 3} × {}, dos dodecaedros paralelos conectados por 12 lados del prisma pentagonal .
• ...

Los politopos prismáticos de orden superior también existen como productos cartesianos de dos politopos cualesquiera. La dimensión de un politopo de producto es el producto de las dimensiones de sus elementos. Los primeros ejemplos de estos existen en el espacio de 4 dimensiones; se denominan duoprismas como el producto de dos polígonos. Los duoprismas regulares se representan como { p } × { q }.

Ver también

• Prisma apeirogonal
• Prisma rectificado
• Prismanes
• Lista de formas

Referencias

1. NW Johnson : Geometrías y transformaciones , (2018) ISBN  978-1-107-10340-5 Capítulo 11: Grupos de simetría finita , 11.3 Pirámides, prismas y antiprismas, figura 11.3b
2. William F. Kern, James R. Bland, Medición sólida con pruebas , 1938, p.28
3. Thomas Malton (1774). Un camino real hacia la geometría: o una introducción fácil y familiar a las matemáticas. ... Por Thomas Malton. ... autor y vendido. págs. 360–.
4. James Elliot (1845). Clave para el tratado completo sobre geometría práctica y medición: que contiene demostraciones completas de las reglas ... Longman, Brown, Green y Longmans. págs. 3–.
5. William F. Kern, James R. Bland, Medición sólida con pruebas , 1938, p.81
6. Los hechos en el archivo: Manual de geometría, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4 , p.172 
7. [1]

• Anthony Pugh (1976). Poliedros: un enfoque visual . California: Universidad de California Press Berkeley. ISBN 0-520-03056-7. Capítulo 2: Poliedros, prismas y antiprismas de Arquímedes

Enlaces externos

• Weisstein, Eric W. "Prism" . MathWorld .
• Modelos en papel de prismas y antiprismas Redes libres de prismas y antiprismas
• Modelos en papel de prismas y antiprismas Utilizando redes generadas por Stella