Función divisor

Función aritmética relacionada con los divisores de un número entero

Función divisor σ ₀ ( n ) hasta n  = 250

Función sigma σ ₁ ( n ) hasta n  = 250

Suma de los cuadrados de los divisores, σ ₂ ( n ), hasta n  = 250

Suma de cubos de divisores, σ ₃ ( n ) hasta n  = 250

En matemáticas , y específicamente en teoría de números , una función divisor es una función aritmética relacionada con los divisores de un número entero . Cuando se hace referencia como la función de divisor, que cuenta el número de divisores de un número entero (incluyendo 1 y el número en sí). Aparece en una serie de identidades notables, incluidas las relaciones en la función zeta de Riemann y la serie de formas modulares de Eisenstein . Las funciones divisorias fueron estudiadas por Ramanujan , quien dio una serie de congruencias importantes yidentidades ; estos se tratan por separado en el artículo Suma de Ramanujan .

Una función relacionada es la función sumatoria del divisor, que, como su nombre lo indica, es una suma sobre la función divisor.

Definición

La función de suma de divisores positivos σ _x ( n ), para un número real o complejo x , se define como la suma de las x- ésimas potencias de los divisores positivos de n . Puede expresarse en notación sigma como

${\displaystyle \sigma _{x}(n)=\sum _{d\mid n}d^{x}\,\!,}$

donde ${\displaystyle {d\mid n}}$es la abreviatura de " d divide n ". Las notaciones d ( n ), ν ( n ) y τ ( n ) (para el alemán Teiler = divisores) también se utilizan para denotar σ ₀ ( n ), o la función de número de divisores ^{[1] [2]} ( OEIS :  A000005 ). Cuando x es 1, la función se llama función sigma o función de suma de divisores , ^{[1] [3]} y el subíndice a menudo se omite, por lo que σ ( n ) es lo mismo que σ ₁( n ) ( OEIS :  A000203 ).

La suma alícuota s ( n ) de n es la suma de los divisores propios (es decir, los divisores excluyendo el propio n , OEIS :  A001065 ), y es igual a σ ₁ ( n ) -  n ; la secuencia de alícuotas de n se forma aplicando repetidamente la función de suma de alícuotas.

Ejemplo

Por ejemplo, σ ₀ (12) es el número de los divisores de 12:

${\displaystyle {\begin{aligned}\sigma _{0}(12)&=1^{0}+2^{0}+3^{0}+4^{0}+6^{0}+12^{0}\\&=1+1+1+1+1+1=6,\end{aligned}}}$

mientras que σ ₁ (12) es la suma de todos los divisores:

${\displaystyle {\begin{aligned}\sigma _{1}(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}+12^{1}\\&=1+2+3+4+6+12=28,\end{aligned}}}$

y la suma alícuota s (12) de los divisores propios es:

${\displaystyle {\begin{aligned}s(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}\\&=1+2+3+4+6=16.\end{aligned}}}$

Tabla de valores

Los casos x = 2 a 5 se enumeran en OEIS :  A001157 - OEIS :  A001160 , x = 6 a 24 se enumeran en OEIS :  A013954 - OEIS :  A013972 .

norte	factorización	σ 0 ( n )	σ 1 ( n )	σ 2 ( n )	σ 3 ( n )	σ 4 ( n )
1	1	1	1	1	1	1
2	2	2	3	5	9	17
3	3	2	4	10	28	82
4	2 2	3	7	21	73	273
5	5	2	6	26	126	626
6	2 × 3	4	12	50	252	1394
7	7	2	8	50	344	2402
8	2 3	4	15	85	585	4369
9	3 2	3	13	91	757	6643
10	2 × 5	4	18	130	1134	10642
11	11	2	12	122	1332	14642
12	2 2 × 3	6	28	210	2044	22386
13	13	2	14	170	2198	28562
14	2 × 7	4	24	250	3096	40834
15	3 × 5	4	24	260	3528	51332
dieciséis	2 4	5	31	341	4681	69905
17	17	2	18	290	4914	83522
18	2 × 3 2	6	39	455	6813	112931
19	19	2	20	362	6860	130322
20	2 2 × 5	6	42	546	9198	170898
21	3 × 7	4	32	500	9632	196964
22	2 × 11	4	36	610	11988	248914
23	23	2	24	530	12168	279842
24	2 3 × 3	8	60	850	16380	358258
25	5 2	3	31	651	15751	391251
26	2 × 13	4	42	850	19782	485554
27	3 3	4	40	820	20440	538084
28	2 2 × 7	6	56	1050	25112	655746
29	29	2	30	842	24390	707282
30	2 × 3 × 5	8	72	1300	31752	872644
31	31	2	32	962	29792	923522
32	2 5	6	63	1365	37449	1118481
33	3 × 11	4	48	1220	37296	1200644
34	2 × 17	4	54	1450	44226	1419874
35	5 × 7	4	48	1300	43344	1503652
36	2 2 × 3 2	9	91	1911	55261	1813539
37	37	2	38	1370	50654	1874162
38	2 × 19	4	60	1810	61740	2215474
39	3 × 13	4	56	1700	61544	2342084
40	2 3 × 5	8	90	2210	73710	2734994
41	41	2	42	1682	68922	2825762
42	2 × 3 × 7	8	96	2500	86688	3348388
43	43	2	44	1850	79508	3418802
44	2 2 × 11	6	84	2562	97236	3997266
45	3 2 × 5	6	78	2366	95382	4158518
46	2 × 23	4	72	2650	109512	4757314
47	47	2	48	2210	103824	4879682
48	2 4 × 3	10	124	3410	131068	5732210
49	7 2	3	57	2451	117993	5767203
50	2 × 5 2	6	93	3255	141759	6651267

Propiedades

Fórmulas en poderes primos

Para un número primo p ,

${\displaystyle {\begin{aligned}\sigma _{0}(p)&=2\\\sigma _{0}(p^{n})&=n+1\\\sigma _{1}(p)&=p+1\end{aligned}}}$

porque, por definición, los factores de un número primo son 1 y él mismo. Además, donde p _n # denota el primorial ,

${\displaystyle \sigma _{0}(p_{n}\#)=2^{n}}$

dado que n factores primos permiten una secuencia de selección binaria (${\displaystyle p_{i}}$o 1) a partir de n términos para cada divisor propio formado.

Claramente, ${\displaystyle 1<\sigma _{0}(n)<n}$ para todos ${\displaystyle n>2}$, y ${\displaystyle \sigma _{x}(n)>n}$ para todos ${\displaystyle n>1}$, ${\displaystyle x>0}$ .

La función divisor es multiplicativa , ^{[ ¿por qué? ]} pero no completamente multiplicativo :

${\displaystyle \gcd(a,b)=1\Longrightarrow \sigma _{x}(ab)=\sigma _{x}(a)\sigma _{x}(b).}$

La consecuencia de esto es que, si escribimos

${\displaystyle n=\prod _{i=1}^{r}p_{i}^{a_{i}}}$

donde r  =  ω ( n ) es el número de factores primos distintos de n , p _i es el i- ésimo factor primo y a _i es la potencia máxima de p _i por la cual n es divisible , entonces tenemos: ^[4]

${\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}\sum _{j=0}^{a_{i}}p_{i}^{jx}=\prod _{i=1}^{r}\left(1+p_{i}^{x}+p_{i}^{2x}+\cdots +p_{i}^{a_{i}x}\right).}$

que, cuando x  ≠ 0, es equivalente a la fórmula útil: ^[4]

${\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}{\frac {p_{i}^{(a_{i}+1)x}-1}{p_{i}^{x}-1}}.}$

Cuando x  = 0, d ( n ) es: ^[4]

${\displaystyle \sigma _{0}(n)=\prod _{i=1}^{r}(a_{i}+1).}$

Por ejemplo, si n es 24, hay dos factores primos ( p ₁ es 2; p ₂ es 3); teniendo en cuenta que 24 es el producto de 2 ³ × 3 ¹ , a ₁ es 3 y a ₂ es 1. Por lo tanto, podemos calcular${\displaystyle \sigma _{0}(24)}$ como tal:

${\displaystyle \sigma _{0}(24)=\prod _{i=1}^{2}(a_{i}+1)=(3+1)(1+1)=4\cdot 2=8.}$

Los ocho divisores contados por esta fórmula son 1, 2, 4, 8, 3, 6, 12 y 24.

Otras propiedades e identidades

Euler demostró la notable recurrencia: ^{[5] [6] [7]}

${\displaystyle {\begin{aligned}\sigma (n)&=\sigma (n-1)+\sigma (n-2)-\sigma (n-5)-\sigma (n-7)+\sigma (n-12)+\sigma (n-15)+\cdots \\&=\sum _{i\in \mathbb {Z} }(-1)^{i+1}\left(\sigma \left(n-{\frac {1}{2}}\left(3i^{2}-i\right)\right)+\sigma \left(n-{\frac {1}{2}}\left(3i^{2}+i\right)\right)\right)\end{aligned}}}$

donde establecemos ${\displaystyle \sigma (0)=n}$ si ocurre y ${\displaystyle \sigma (i)=0}$ por ${\displaystyle i\leq 0,}$ ${\displaystyle {\tfrac {1}{2}}\left(3i^{2}-i\right)}$son los números pentagonales . De hecho, Euler demostró esto mediante la diferenciación logarítmica de la identidad en su teorema del número pentagonal .

Para un número entero no cuadrado, n , cada divisor, d , de n se empareja con el divisor n / d de n y${\displaystyle \sigma _{0}(n)}$incluso; para un entero cuadrado, un divisor (a saber${\displaystyle {\sqrt {n}}}$) no está emparejado con un divisor distinto y ${\displaystyle \sigma _{0}(n)}$es impar. Del mismo modo, el número${\displaystyle \sigma _{1}(n)}$es impar si y solo si n es un cuadrado o dos veces un cuadrado. ^{[ cita requerida ]}

También notamos s ( n ) = σ ( n ) -  n . Aquí s ( n ) denota la suma de los divisores propios de n , es decir, los divisores de n excluyendo n él mismo. Esta función es la que se utiliza para reconocer números perfectos que son los n para los cuales s ( n ) =  n . Si s ( n )> n entonces n es un número abundante y si s ( n) < n entonces n es un número deficiente .

Si n es una potencia de 2, por ejemplo, ${\displaystyle n=2^{k}}$, luego ${\displaystyle \sigma (n)=2\cdot 2^{k}-1=2n-1,}$y s (n) = n - 1 , lo que hace que n sea casi perfecto .

Como ejemplo, para dos números primos distintos p y q con p <q , dejar

${\displaystyle n=pq.}$

Luego

${\displaystyle \sigma (n)=(p+1)(q+1)=n+1+(p+q),}$

${\displaystyle \varphi (n)=(p-1)(q-1)=n+1-(p+q),}$

y

${\displaystyle n+1=(\sigma (n)+\varphi (n))/2,}$

${\displaystyle p+q=(\sigma (n)-\varphi (n))/2,}$

donde ${\displaystyle \varphi (n)}$es la función totient de Euler .

Entonces, las raíces de:

${\displaystyle (x-p)(x-q)=x^{2}-(p+q)x+n=x^{2}-[(\sigma (n)-\varphi (n))/2]x+[(\sigma (n)+\varphi (n))/2-1]=0}$

nos permiten expresar p y q en términos de σ ( n ) y φ ( n ) únicamente, sin saber siquiera n o p + q , como:

${\displaystyle p=(\sigma (n)-\varphi (n))/4-{\sqrt {[(\sigma (n)-\varphi (n))/4]^{2}-[(\sigma (n)+\varphi (n))/2-1]}},}$

${\displaystyle q=(\sigma (n)-\varphi (n))/4+{\sqrt {[(\sigma (n)-\varphi (n))/4]^{2}-[(\sigma (n)+\varphi (n))/2-1]}}.}$

Además, sabiendo n y cualquiera ${\displaystyle \sigma (n)}$ o ${\displaystyle \varphi (n)}$ (o conociendo p + q y ya sea ${\displaystyle \sigma (n)}$ o ${\displaystyle \varphi (n)}$) nos permite encontrar fácilmente p y q .

En 1984, Roger Heath-Brown demostró que la igualdad

${\displaystyle \sigma _{0}(n)=\sigma _{0}(n+1)}$

es cierto para una infinidad de valores de n, consulte OEIS :  A005237 .

Relaciones de serie

Dos series de Dirichlet que involucran la función divisor son: ^[8]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}=\zeta (s)\zeta (s-a)\quad {\text{for}}\quad s>1,s>a+1,}$

que para d ( n ) =  σ ₀ ( n ) da: ^[8]

${\displaystyle \sum _{n=1}^{\infty }{\frac {d(n)}{n^{s}}}=\zeta ^{2}(s)\quad {\text{for}}\quad s>1,}$

y ^[9]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}}={\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}}.}$

Una serie de Lambert que involucra la función divisor es: ^[10]

${\displaystyle \sum _{n=1}^{\infty }q^{n}\sigma _{a}(n)=\sum _{n=1}^{\infty }\sum _{j=1}^{\infty }n^{a}q^{j\,n}=\sum _{n=1}^{\infty }{\frac {n^{a}q^{n}}{1-q^{n}}}}$

para complejo arbitrario | q | ≤ 1 y  a . Esta suma también aparece como la serie de Fourier de la serie de Eisenstein y las invariantes de las funciones elípticas de Weierstrass .

Para ${\displaystyle k>0}$existe una representación de serie explícita con sumas de Ramanujan ${\displaystyle c_{m}(n)}$como: ^[11]

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\sum _{m=1}^{\infty }{\frac {c_{m}(n)}{m^{k+1}}}.}$

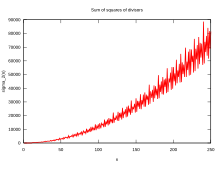
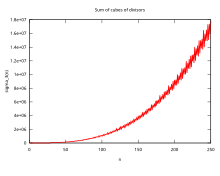
El cálculo de los primeros términos de ${\displaystyle c_{m}(n)}$ muestra sus oscilaciones en torno al "valor medio" ${\displaystyle \zeta (k+1)n^{k}}$:

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\left[1+{\frac {(-1)^{n}}{2^{k+1}}}+{\frac {2\cos {\frac {2\pi n}{3}}}{3^{k+1}}}+{\frac {2\cos {\frac {\pi n}{2}}}{4^{k+1}}}+\cdots \right]}$

Tasa de crecimiento

En notación pequeña-o , la función divisor satisface la desigualdad: ^{[12] [13]}

${\displaystyle {\mbox{for all }}\varepsilon >0,\quad d(n)=o(n^{\varepsilon }).}$

Más precisamente, Severin Wigert demostró que: ^[13]

${\displaystyle \limsup _{n\to \infty }{\frac {\log d(n)}{\log n/\log \log n}}=\log 2.}$

Por otro lado, dado que hay infinitos números primos , ^[13]

${\displaystyle \liminf _{n\to \infty }d(n)=2.}$

En notación Big-O , Peter Gustav Lejeune Dirichlet mostró que el orden promedio de la función divisor satisface la siguiente desigualdad: ^{[14] [15]}

${\displaystyle {\mbox{for all }}x\geq 1,\sum _{n\leq x}d(n)=x\log x+(2\gamma -1)x+O({\sqrt {x}}),}$

donde ${\displaystyle \gamma }$es la constante gamma de Euler . Mejorando el límite${\displaystyle O({\sqrt {x}})}$en esta fórmula se conoce como problema del divisor de Dirichlet .

El comportamiento de la función sigma es irregular. La tasa de crecimiento asintótica de la función sigma se puede expresar mediante: ^[16]

${\displaystyle \limsup _{n\rightarrow \infty }{\frac {\sigma (n)}{n\,\log \log n}}=e^{\gamma },}$

donde lim sup es el límite superior . Este resultado es el teorema de Grönwall , publicado en 1913 ( Grönwall 1913 ). Su demostración usa el tercer teorema de Mertens , que dice que:

${\displaystyle \lim _{n\to \infty }{\frac {1}{\log n}}\prod _{p\leq n}{\frac {p}{p-1}}=e^{\gamma },}$

donde p denota un primo.

En 1915, Ramanujan demostró que bajo el supuesto de la hipótesis de Riemann , la desigualdad:

${\displaystyle \ \sigma (n)<e^{\gamma }n\log \log n}$ (La desigualdad de Robin)

se cumple para todos los n suficientemente grandes ( Ramanujan 1997 ). El mayor valor conocido que viola la desigualdad es n = 5040 . En 1984, Guy Robin demostró que la desigualdad es cierta para todo n > 5040 si y solo si la hipótesis de Riemann es cierta ( Robin 1984 ). Este es el teorema de Robin y la desigualdad se conoció después de él. Robin además demostró que si la hipótesis de Riemann es falsa, entonces hay un número infinito de valores de n que violan la desigualdad, y se sabe que el más pequeño de tales n > 5040 debe ser superabundante (Akbary y Friggstad 2009 ). Se ha demostrado que la desigualdad es válida para enteros grandes impares y libres de cuadrados, y que la hipótesis de Riemann es equivalente a la desigualdad solo para n divisible por la quinta potencia de un primo ( Choie et al. 2007 ).

Robin también demostró, incondicionalmente, que la desigualdad:

${\displaystyle \ \sigma (n)<e^{\gamma }n\log \log n+{\frac {0.6483\ n}{\log \log n}}}$

se mantiene para todo n ≥ 3.

Jeffrey Lagarias dio un límite relacionado en 2002, quien demostró que la hipótesis de Riemann es equivalente a la afirmación de que:

${\displaystyle \sigma (n)<H_{n}+\log(H_{n})e^{H_{n}}}$

para cada número natural n > 1, donde${\displaystyle H_{n}}$es el n- ésimo número armónico , ( Lagarias 2002 ).

Ver también

• Convoluciones de suma de divisores Enumera algunas identidades que involucran las funciones de divisor
• Función totient de Euler (función phi de Euler)
• Número refactorable
• Tabla de divisores
• Divisor unitario

Notas

1. Long (1972 , p. 46)
2. Pettofrezzo y Byrkit (1970 , p. 63)
3. Pettofrezzo y Byrkit (1970 , p. 58)
4. Hardy y Wright (2008) , págs. 310 y sig., §16.7.
5. Euler, Leonhard; Bell, Jordan (2004). "Una observación sobre las sumas de divisores". arXiv : matemáticas / 0411587 .
6. http://eulerarchive.maa.org//pages/E175.html , Decouverte d'une loi tout extraordinaire des nombres par rapport a la somme de leurs diviseurs
7. https://scholarlycommons.pacific.edu/euler-works/542/ , De mirabilis proprietatibus numerorum pentagonalium
8. Hardy y Wright (2008) , págs. 326-328, §17.5.
9. Hardy y Wright (2008) , págs. 334-337, §17.8.
10. Hardy y Wright (2008) , págs. 338-341, §17.10.
11. E. Krätzel (1981). Zahlentheorie . Berlín: VEB Deutscher Verlag der Wissenschaften. pag. 130. (Alemán)
12. Apostol (1976) , p. 296.error sfnp: sin destino: CITEREFApostol1976 ( ayuda )
13. Hardy y Wright (2008) , págs. 342-347, §18.1.
14. Apostol (1976) , Teorema 3.3.error sfnp: sin destino: CITEREFApostol1976 ( ayuda )
15. Hardy y Wright (2008) , págs. 347-350, §18.2.
16. Hardy y Wright (2008) , págs. 469-471, §22.9.

Referencias

• Akbary, Amir; Friggstad, Zachary (2009), "Números superabundantes y la hipótesis de Riemann" (PDF) , American Mathematical Monthly , 116 (3): 273-275, doi : 10.4169 / 193009709X470128 , archivado desde el original (PDF) el 2014-04- 11.
• Apostol, Tom M. (1976), Introducción a la teoría analítica de números , Textos de pregrado en matemáticas, Nueva York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR  0434929 , Zbl  0.335,10001
• Bach, Eric ; Shallit, Jeffrey , Teoría algorítmica de números , volumen 1, 1996, MIT Press. ISBN 0-262-02405-5 , consulte la página 234 en la sección 8.8. 
• Caveney, Geoffrey; Nicolas, Jean-Louis ; Sondow, Jonathan (2011), "Teorema de Robin, números primos y una nueva reformulación elemental de la hipótesis de Riemann" (PDF) , INTEGERS: The Electronic Journal of Combinatorial Number Theory , 11 : A33, arXiv : 1110.5078 , Bibcode : 2011arXiv1110.5078C
• Choie, YoungJu ; Lichiardopol, Nicolas; Moree, Pieter ; Solé, Patrick (2007), "Sobre el criterio de Robin para la hipótesis de Riemann", Journal de théorie des nombres de Bordeaux , 19 (2): 357–372, arXiv : math.NT / 0604314 , doi : 10.5802 / jtnb.591 , ISSN  1246-7405 , MR  2394891 , S2CID  3.207.238 , Zbl  1163.11059
• Grönwall, Thomas Hakon (1913), "Algunas expresiones asintóticas en la teoría de los números", Transactions of the American Mathematical Society , 14 : 113-122, doi : 10.1090 / S0002-9947-1913-1500940-6
• Hardy, GH ; Wright, EM (2008) [1938], Introducción a la teoría de los números , revisada por DR Heath-Brown y JH Silverman . Prólogo de Andrew Wiles . (6a ed.), Oxford: Oxford University Press , ISBN 978-0-19-921986-5, MR  2445243 , Zbl  1159.11001
• Ivić, Aleksandar (1985), La función zeta de Riemann. La teoría de la función zeta de Riemann con aplicaciones , A Wiley-Interscience Publication, Nueva York, etc .: John Wiley & Sons, págs. 385–440, ISBN 0-471-80634-X, Zbl  0556.10026
• Lagarias, Jeffrey C. (2002), "Un problema elemental equivalente a la hipótesis de Riemann", The American Mathematical Monthly , 109 (6): 534–543, arXiv : math / 0008177 , doi : 10.2307 / 2695443 , ISSN  0002-9890 , JSTOR  2695443 , MR  1908008 , S2CID  15884740
• Long, Calvin T. (1972), Introducción elemental a la teoría de números (2a ed.), Lexington: DC Heath and Company , LCCN  77171950
• Pettofrezzo, Anthony J .; Byrkit, Donald R. (1970), Elementos de la teoría de números , Englewood Cliffs: Prentice Hall , LCCN  77081766
• Ramanujan, Srinivasa (1997), "Números altamente compuestos, anotados por Jean-Louis Nicolas y Guy Robin", The Ramanujan Journal , 1 (2): 119-153, doi : 10.1023 / A: 1009764017495 , ISSN  1382-4090 , MR  1606180 , S2CID  115619659
• Robin, Guy (1984), "Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann", Journal de Mathématiques Pures et Appliquées , Neuvième Série, 63 (2): 187–213, ISSN  0021-7824 , MR  0774171
• Williams, Kenneth S. (2011), Teoría de números en el espíritu de Liouville , Textos de estudiantes de la Sociedad Matemática de Londres, 76 , Cambridge: Cambridge University Press , ISBN 978-0-521-17562-3, Zbl  1227.11002

Enlaces externos

• Weisstein, Eric W. "Función de divisor" . MathWorld .
• Weisstein, Eric W. "Teorema de Robin" . MathWorld .
• Evaluación elemental de ciertas sumas de convolución que involucran funciones divisorias PDF de un artículo de Huard, Ou, Spearman y Williams. Contiene pruebas elementales (es decir, que no se basan en la teoría de las formas modulares) de las convoluciones de suma de divisores, fórmulas para el número de formas de representar un número como una suma de números triangulares y resultados relacionados.