Objeto dual

En la teoría de categorías , una rama de las matemáticas , un objeto dual es un análogo de un espacio vectorial dual del álgebra lineal para objetos en categorías monoidales arbitrarias . Es sólo una generalización parcial, basada en las propiedades categóricas de la dualidad para espacios vectoriales de dimensión finita . Un objeto que admite un dual se denomina objeto dualizable . En este formalismo, los espacios vectoriales de dimensión infinita no son dualizables, ya que el espacio vectorial dual V ^∗ no satisface los axiomas. ^[1]A menudo, un objeto es dualizable solo cuando satisface alguna propiedad de finitud o compacidad. ^[2]

Una categoría en la que cada objeto tiene un dual se llama autónoma o rígida . La categoría de espacios vectoriales de dimensión finita con el producto tensorial estándar es rígida, mientras que la categoría de todos los espacios vectoriales no lo es.

Motivación

Deje V un espacio vectorial de dimensión finita sobre algún campo K . La noción estándar de un espacio vectorial dual V ^∗ tiene la siguiente propiedad: para cualquier K -espacios vectorial U y W hay una adjunción Hom _K ( U ⊗ V , W ) = Hom _K ( U , V ^∗ ⊗ W ), y esto caracteriza a V ^∗ hasta un isomorfismo único. Esta expresión tiene sentido en cualquier categoría con un reemplazo apropiado para el producto tensorial de espacios vectoriales. Para cualquier categoría monoidal ( C , ⊗) se puede intentar definir un dual de un objeto V como un objeto V ^∗ ∈ C con un isomorfismo natural de bifunctores

Hom _C ((-) ₁ ⊗ V , (-) ₂ ) → Hom _C ((-) ₁ , V ^∗ ⊗ (-) ₂ )

Para una noción de dualidad que se comporte bien, este mapa no solo debe ser natural en el sentido de la teoría de categorías, sino también respetar la estructura monoidal de alguna manera. ^{[1] Por tanto,} una definición real de un objeto dual es más complicada.

En una categoría monoidal cerrada C , es decir, una categoría monoidal con un functor Hom interno , un enfoque alternativo es simular la definición estándar de un espacio vectorial dual como un espacio de funcionales . Para un objeto V ∈ C, defina V ^∗ como${\displaystyle {\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})}$, donde 1 _C es la identidad monoidal. En algunos casos, este objeto será un objeto dual de V en el sentido anterior, pero en general conduce a una teoría diferente. ^[3]

Definición

Considere un objeto ${\displaystyle X}$en una categoría monoidal ${\displaystyle (\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )}$. El objeto${\displaystyle X^{*}}$se llama dual izquierdo de${\displaystyle X}$ si existen dos morfismos

${\displaystyle \eta :I\to X\otimes X^{*}}$, llamado coevaluación , y${\displaystyle \varepsilon :X^{*}\otimes X\to I}$, llamado la evaluación ,

de manera que los dos diagramas siguientes conmuten:

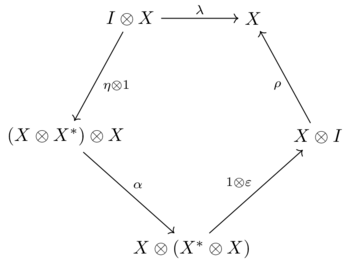y

El objeto ${\displaystyle X}$se llama el dual derecho de${\displaystyle X^{*}}$. Esta definición se debe a Dold y Puppe (1980) .

Los duales izquierdos son canónicamente isomórficos cuando existen, al igual que los duales derechos. Cuando C está trenzado (o simétrico ), cada dual izquierdo es también un dual derecho, y viceversa.

Si consideramos una categoría monoidal como una bicategoría con un objeto, un par dual es exactamente un par adjunto .

Ejemplos

• Considere una categoría monoidal (Vect _K , ⊗ _K ) de espacios vectoriales sobre un campo K con el producto tensorial estándar. Un espacio V es dualizable si y solo si es de dimensión finita, y en este caso el objeto dual V ^∗ coincide con la noción estándar de un espacio vectorial dual .
• Considere una categoría monoidal (Mod _R , ⊗ _R ) de módulos sobre un anillo conmutativo R con el producto tensorial estándar . Un módulo M es dualizable si y solo si es un módulo proyectivo generado de forma finita . En ese caso, el objeto dual M ^∗ también viene dado por el módulo de homomorfismos Hom _R ( M , R ).
• Considere una categoría de homotopía de espectros puntiagudos Ho (Sp) con el producto de rotura como estructura monoidal. Si M es un barrio compacto , se retrae en ${\displaystyle \mathbb {R} ^{n}}$(por ejemplo, una variedad compacta y suave ), entonces el espectro puntiagudo correspondiente Σ ^∞ ( M ⁺ ) es dualizable. Esto es una consecuencia de la dualidad Spanier-Whitehead , que implica en particular la dualidad de Poincaré para variedades compactas. ^[1]
• La categoría ${\displaystyle \mathrm {End} (\mathbf {C} )}$de endofunctores de una categoría${\displaystyle \mathbf {C} }$es una categoría monoidal según la composición de los functores . Un functor${\displaystyle F}$ es un dual izquierdo de un funtor ${\displaystyle G}$ si ${\displaystyle F}$ se deja adjunto a ${\displaystyle G}$. ^[4]

Categorías con duales

Una categoría monoidal en la que cada objeto tiene un dual izquierdo (respectivamente derecho) a veces se denomina categoría autónoma izquierda (respectivamente derecha) . Los geómetras algebraicos lo llaman categoría rígida izquierda (respectivamente derecha) . Una categoría monoidal donde cada objeto tiene un dual izquierdo y uno derecho se llama categoría autónoma . Una categoría autónoma que también es simétrica se denomina categoría cerrada compacta .

Rastros

Cualquier endomorphism f de un objeto dualizable admite un rastro , que es un cierto endomorphism de la unidad monoidal de C . Esta noción incluye, como casos muy especiales, la traza en álgebra lineal y la característica de Euler de un complejo de cadenas .

Ver también

• Objeto de dualización

Referencias

1. Ponto, Kate; Shulman, Michael (2014). "Rastros en categorías monoidales simétricas". Expositiones Mathematicae . 32 (3): 248-273. arXiv : 1107.6032 . Código Bibliográfico : 2011arXiv1107.6032P .
2. Becker, James C .; Gottlieb, Daniel Henry (1999). "Una historia de dualidad en topología algebraica" (PDF) . En James, IM (ed.). Historia de la topología . Holanda Septentrional. págs. 725–745. ISBN  9780444823755.
3. "objeto dual en una categoría cerrada en nLab" . ncatlab.org . Consultado el 11 de diciembre de 2017 .
4. Véase, por ejemplo, el ejercicio 2.10.4 en Pavel Eting de "Categorías de tensores".

• Dold, Albrecht; Puppe, Dieter (1980), "Duality, trace, and transfer", Actas de la Conferencia Internacional sobre Topología Geométrica (Varsovia, 1978) , PWN, Varsovia, págs. 81-102, MR  0656721
• Peter Freyd y David Yetter (1989). "Categorías cerradas compactas trenzadas con aplicaciones a topología de dimensiones reducidas" . Avances en Matemáticas . 77 (2): 156–182. doi : 10.1016 / 0001-8708 (89) 90018-2 .
• André Joyal y Ross Street . "La geometría del cálculo tensorial II". Biblioteca de síntesis . 259 : 29–68.

Este artículo relacionado con la teoría de categorías es un fragmento . Puedes ayudar a Wikipedia expandiéndolo .

• v
• t
• mi