Valores propios y vectores propios
En álgebra lineal , un vector propio ( ) o vector característico de una transformación lineal es un vector distinto de cero que cambia como máximo en un factor escalar cuando se le aplica esa transformación lineal. El valor propio correspondiente , a menudo denotado por , es el factor por el cual se escala el vector propio.
Geométricamente , un vector propio, correspondiente a un valor propio real distinto de cero, apunta en una dirección en la que se estira por la transformación y el valor propio es el factor por el cual se estira. Si el valor propio es negativo, la dirección se invierte. En términos generales, en un espacio vectorial multidimensional , el vector propio no se gira.
Si T es una transformación lineal de un espacio vectorial V sobre un campo F en sí mismo y v es un vector distinto de cero en V , entonces v es un vector propio de T si T ( v ) es un múltiplo escalar de v . Esto se puede escribir como
donde λ es un escalar en F , conocido como valor propio , valor característico o raíz característica asociada con v .
Existe una correspondencia directa entre matrices cuadradas de n por n y transformaciones lineales de un espacio vectorial de n dimensiones en sí mismo, dada cualquier base del espacio vectorial. Por lo tanto, en un espacio vectorial de dimensión finita, es equivalente a definir valores propios y vectores propios utilizando el lenguaje de matrices o el lenguaje de transformaciones lineales.
Los valores propios y los vectores propios ocupan un lugar destacado en el análisis de transformaciones lineales. El prefijo eigen- se adopta de la palabra alemana eigen ( cognado con la palabra inglesa own ) para "propio", "característico", "propio". [6] Utilizados originalmente para estudiar los ejes principales del movimiento de rotación de cuerpos rígidos , los valores propios y los vectores propios tienen una amplia gama de aplicaciones, por ejemplo, en análisis de estabilidad, análisis de vibraciones , orbitales atómicos , reconocimiento facial ydiagonalización de la matriz .
En este
mapeo de corte, la flecha roja cambia de dirección, pero la flecha azul no. La flecha azul es un vector propio de este mapeo de corte porque no cambia de dirección y, dado que su longitud no cambia, su valor propio es 1.
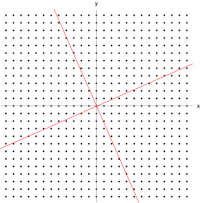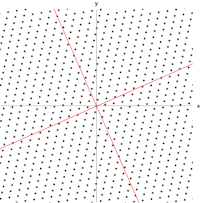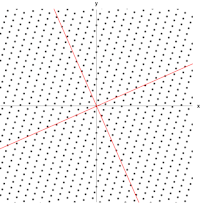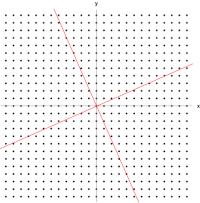
Una matriz real y simétrica de 2×2 representa un estiramiento y corte del plano. Los vectores propios de la matriz (líneas rojas) son las dos direcciones especiales tales que cada punto sobre ellas simplemente se deslizará sobre ellas.
La matriz
A actúa estirando el vector
x , sin cambiar su dirección, por lo que
x es un vector propio de
A. La matriz de transformación
A = conserva la dirección de los vectores morados paralelos a
v λ =1 = [1 −1]
T y los vectores azules paralelos a
v λ =3 = [1 1]
T . Los vectores rojos no son paralelos a ninguno de los vectores propios, por lo que la transformación cambia sus direcciones. Las longitudes de los vectores violetas no cambian después de la transformación (debido a su valor propio de 1), mientras que los vectores azules tienen una longitud tres veces mayor que la original (debido a su valor propio de 3). Ver también:
Una versión extendida, que muestra los cuatro cuadrantes .
Las funciones de onda asociadas con los estados ligados de un electrón en un átomo de hidrógeno pueden verse como los vectores propios del hamiltoniano del átomo de hidrógeno , así como del operador de momento angular . Están asociados con valores propios interpretados como sus energías (aumentando hacia abajo: ) y momento angular (aumentando a través de: s, p, d, …). La ilustración muestra el cuadrado del valor absoluto de las funciones de onda. Las áreas más brillantes corresponden a una mayor densidad de probabilidad para una medición de posición . El centro de cada figura es el núcleo atómico , un protón .
.
PCA de la distribución gaussiana multivariante centrada en con una desviación estándar de 3 en aproximadamente la dirección y de 1 en la dirección ortogonal. Los vectores que se muestran son vectores propios unitarios de la matriz de covarianza (simétrica, semidefinida positiva) escalada por la raíz cuadrada del valor propio correspondiente. Al igual que en el caso unidimensional, se toma la raíz cuadrada porque la desviación estándar se visualiza más fácilmente que la varianza .
Forma modal de un diapasón a frecuencia propia 440,09 Hz
Caras propias como ejemplos de vectores propios
![{\displaystyle \left[{\begin{pequeña matriz}2&1\\1&2\end{pequeña matriz}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
