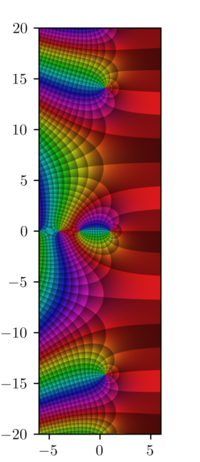
Función zeta de Riemann
La función zeta de Riemann o función zeta de Euler-Riemann , denotada por la letra griega ζ ( zeta ), es una función matemática de una variable compleja definida como
La función zeta de Riemann juega un papel fundamental en la teoría analítica de números y tiene aplicaciones en física , teoría de probabilidad y estadística aplicada .
Leonhard Euler introdujo y estudió por primera vez la función sobre los reales en la primera mitad del siglo XVIII. El artículo de Bernhard Riemann de 1859 " Sobre el número de primos menores que una magnitud dada " amplió la definición de Euler a una variable compleja , probó su continuación meromórfica y su ecuación funcional , y estableció una relación entre sus ceros y la distribución de números primos . Este documento también contenía la hipótesis de Riemann , una conjeturasobre la distribución de ceros complejos de la función zeta de Riemann que es considerada por muchos matemáticos como el problema sin resolver más importante de las matemáticas puras . [3]
Euler calculó los valores de la función zeta de Riemann en números enteros positivos. El primero de ellos, ζ (2) , proporciona una solución al problema de Basilea . En 1979 Roger Apéry demostró la irracionalidad de ζ (3) . Los valores en los puntos enteros negativos, también encontrados por Euler, son números racionales y juegan un papel importante en la teoría de las formas modulares . Se conocen muchas generalizaciones de la función zeta de Riemann, como las series de Dirichlet , las funciones L de Dirichlet y las funciones L.
La función zeta de Riemann ζ ( s ) es una función de una variable compleja s = σ + it . (La notación s , σ y t se usa tradicionalmente en el estudio de la función zeta, siguiendo a Riemann). Cuando Re( s ) = σ > 1 , la función se puede escribir como una sumatoria convergente o integral:
es la función gamma . La función zeta de Riemann se define para otros valores complejos a través de la continuación analítica de la función definida para σ > 1 .