| Conjunto de antiprismas n -gonales uniformes | |
|---|---|
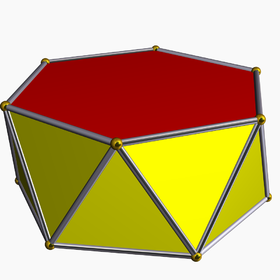 Ejemplo de antiprisma hexagonal uniforme | |
| Escribe | uniforme en el sentido de poliedro semirregular |
| Caras | 2 { n } + 2 n {3} |
| Bordes | 4 n |
| Vértices | 2 n |
| Notación de poliedro de Conway | Un n |
| Configuración de vértice | 3.3.3. norte |
| Símbolo de Schläfli | {} ⊗ { n } [1] s {2,2 n } sr {2, n } |
| Diagramas de Coxeter | |
| Grupo de simetría | D n d , [2 + , 2 n ], (2 * n ), orden 4 n |
| Grupo de rotacion | D n , [2, n ] + , (22 n ), orden 2 n |
| Poliedro doble | trapezoedro convexo dual-uniforme n -gonal |
| Propiedades | caras poligonales regulares , convexas , transitivas a vértices , bases congruentes y coaxiales |
| Neto |  Ejemplo de red antiprisma enneagonal uniforme (n = 9) |
En geometría , un antiprisma n -gonal o n- antiprisma es un poliedro compuesto por dos copias directas paralelas (no imágenes especulares) de un polígono de n lados , conectados por una banda alterna de 2 n triángulos .
Los antiprismas son una subclase de prismatoides y son un tipo (degenerado) de poliedro chato .
Los antiprismas son similares a los prismas , excepto que las bases están torcidas entre sí y que las caras laterales (que conectan las bases) son 2 n triángulos, en lugar de n cuadriláteros.
Antiprisma de derecha
Para un antiprisma con bases regulares de n- gones , generalmente se considera el caso en el que estas dos copias están torcidas en un ángulo de180/norte grados.
El eje de un polígono regular es la línea perpendicular al plano del polígono y que se encuentra en el centro del polígono.
Para un antiprisma con bases regulares n-gon congruentes , torcido por un ángulo de180/nortegrados, se obtiene más regularidad si las bases tienen el mismo eje: son coaxiales ; es decir (para bases no coplanares ): si la línea que conecta los centros de la base es perpendicular a los planos de la base. Entonces, el antiprisma se llama antiprisma recto y sus 2 n caras laterales son triángulos isósceles .
Antiprisma uniforme
Un antiprisma uniforme tiene dos caras de base n-gon regulares congruentes y 2 n triángulos equiláteros como caras laterales.
Los antiprismas uniformes forman una clase infinita de poliedros transitivos de vértice, al igual que los prismas uniformes. Para n = 2 , tenemos el tetraedro regular como antiprisma digonal (antiprisma degenerado); para n = 3 , el octaedro regular como un antiprisma triangular ( antiprisma no degenerado).
Los poliedros duales de los antiprismas son los trapezoedros .
Se discutió la existencia de antiprismas y su nombre fue acuñado por Johannes Kepler , aunque es posible que fueran conocidos previamente por Arquímedes , ya que satisfacen las mismas condiciones en caras y vértices que los sólidos de Arquímedes .
| Nombre antiprisma | Antiprisma digital | (Trigonal) Antiprisma triangular | (Tetragonal) Antiprisma cuadrado | Antiprisma pentagonal | Antiprisma hexagonal | Antiprisma heptagonal | Antiprisma octogonal | Antiprisma enneagonal | Antiprisma decagonal | Antiprisma hedecagonal | Antiprisma dodecagonal | ... | Antiprisma apeirogonal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Imagen de poliedro | ... | ||||||||||||
| Imagen de mosaico esférico | Imagen de mosaico plano | ||||||||||||
| Vertex config. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 |
Diagramas de Schlegel
 A3 |  A4 |  A5 |  A6 |  A7 |  A8 |
Coordenadas cartesianas
Las coordenadas cartesianas para los vértices de un antiprisma derecho (es decir, con bases regulares de n- gones y caras laterales isósceles) son
con k comprendido entre 0 y 2 n - 1;
si los triángulos son equiláteros, entonces
Volumen y superficie
Sea a la longitud del borde de un antiprisma uniforme ; entonces el volumen es
y la superficie es
Poliedros relacionados
Hay un conjunto infinito de antiprismas truncados , incluida una forma de simetría inferior del octaedro truncado (antiprisma triangular truncado). Éstos se pueden alternar para crear antiprismas de desaire , dos de los cuales son sólidos de Johnson , y el antiprisma triangular de desaire es una forma de simetría más baja del icosaedro .
| Antiprismas | ||||
|---|---|---|---|---|
 |  |  |  | ... |
| s {2,4} | s {2,6} | s {2,8} | s {2,10} | s {2,2 n } |
| Antiprismas truncados | ||||
 |  |  |  | ... |
| ts {2,4} | ts {2,6} | ts {2,8} | ts {2,10} | ts {2,2n} |
| Antiprismas desairados | ||||
| J 84 | Icosaedro | J 85 | Caras irregulares ... | |
 |  |  | ... | |
| ss {2,4} | ss {2,6} | ss {2,8} | ss {2,10} | ss {2,2n} |
Simetría
El grupo de simetría de un antiprisma n derecho (es decir, con bases regulares y caras laterales isósceles) es D n d de orden 4 n , excepto en los casos de:
- n = 2: el tetraedro regular , que tiene el grupo de simetría más grande T d de orden 24 = 3 × (4 × 2), que tiene tres versiones de D 2d como subgrupos;
- n = 3: el octaedro regular , que tiene el grupo de simetría más grande O h de orden 48 = 4 × (4 × 3), que tiene cuatro versiones de D 3d como subgrupos.
El grupo de simetría contiene inversión si y solo si n es impar.
El grupo de rotación es D n de orden 2 n , excepto en los casos de:
- n = 2: el tetraedro regular, que tiene el grupo de rotación más grande T de orden 12 = 3 × (2 × 2), que tiene tres versiones de D 2 como subgrupos;
- n = 3: el octaedro regular, que tiene el grupo de rotación más grande O de orden 24 = 4 × (2 × 3), que tiene cuatro versiones de D 3 como subgrupos.
Antiprisma de estrellas
 5/2-antiprisma | 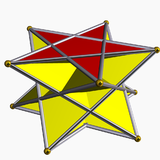 5/3-antiprisma | ||||
 9/2-antiprisma |  9/4-antiprisma |  9/5-antiprisma | |||
Los antiprismas estelares uniformes se nombran por sus bases poligonales estelares , { p / q }, y existen en soluciones progradas y retrógradas (cruzadas). Las formas cruzadas tienen vértices que se cruzan y se indican mediante fracciones "invertidas": p / ( p - q ) en lugar de p / q ; ejemplo: 5/3 en lugar de 5/2.
A antiprisma estrella derecha tiene dos congruente coaxiales regulares convexos o estrella de polígono caras de base, y 2 n triángulo isósceles caras laterales.
Cualquier antiprisma de estrella con bases de polígono de estrella o convexo regular puede convertirse en un antiprisma de estrella correcto (traduciendo y / o torciendo una de sus bases, si es necesario).
En las formas retrógradas, pero no en las formas progradas, los triángulos que unen las bases convexas o estelares cruzan el eje de simetría rotacional. Por lo tanto:
- Los antiprismas de estrellas retrógrados con bases poligonales convexas regulares no pueden tener todas las longitudes de los bordes iguales, por lo que no pueden ser uniformes. "Excepción": un antiprisma de estrella retrógrado con bases de triángulo equilátero (configuración de vértice: 3.3 / 2.3.3) puede ser uniforme; pero luego, tiene la apariencia de un triángulo equilátero: es un poliedro estrella degenerado.
- De manera similar, algunos antiprismas de estrellas retrógradas con bases de polígono de estrellas regulares no pueden tener todas las longitudes de borde iguales, por lo que no pueden ser uniformes. Ejemplo: un antiprisma de estrellas retrógradas con bases regulares de estrellas de 7/5 gon (configuración de vértice: 3.3.3.7/5) no puede ser uniforme.
Asimismo, los compuestos Antiprism estrella con la estrella regular de p / q -gon bases pueden construirse si p y q tienen factores comunes. Ejemplo: una estrella 10/4-antiprisma es el compuesto de dos estrellas 5/2-antiprismas.
| Grupo de simetría | Estrellas uniformes | Estrellas correctas | |||
|---|---|---|---|---|---|
| D4d [2+,8] (2*4) |  3.3/2.3.4 | ||||
| D5h [2,5] (*225) |  3.3.3.5/2 |  3.3/2.3.5 | |||
| D5d [2+,10] (2*5) |  3.3.3.5/3 | ||||
| D6d [2+,12] (2*6) | 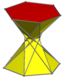 3.3/2.3.6 | ||||
| D7h [2,7] (*227) |  3.3.3.7/2 |  3.3.3.7/4 | |||
| D7d [2+,14] (2*7) |  3.3.3.7/3 | ||||
| D8d [2+,16] (2*8) |  3.3.3.8/3 |  3.3.3.8/5 | |||
| D9h [2,9] (*229) |  3.3.3.9/2 |  3.3.3.9/4 | |||
| D9d [2+,18] (2*9) |  3.3.3.9/5 | ||||
| D10d [2+,20] (2*10) |  3.3.3.10/3 | ||||
| D11h [2,11] (*2.2.11) |  3.3.3.11/2 |  3.3.3.11/4 |  3.3.3.11/6 | ||
| D11d [2+,22] (2*11) |  3.3.3.11/3 |  3.3.3.11/5 |  3.3.3.11/7 | ||
| D12d [2+,24] (2*12) |  3.3.3.12/5 |  3.3.3.12/7 | |||
| ... | ... | ||||
Ver también
- Antiprisma apeirogonal
- Antiprisma rectificado
- Gran antiprisma : un politopo de cuatro dimensiones
- One World Trade Center , un edificio que consta principalmente de un antiprisma cuadrado alargado
- Polígono sesgado
Referencias
- Anthony Pugh (1976). Poliedros: un enfoque visual . California: Universidad de California Press Berkeley. ISBN 0-520-03056-7. Capítulo 2: Poliedros, prismas y antiprismas de Arquímedes
- ^ NW Johnson : Geometrías y transformaciones , (2018) ISBN 978-1-107-10340-5 Capítulo 11: Grupos de simetría finita , 11.3 Pirámides, prismas y antiprismas, Figura 11.3c
Enlaces externos
- Weisstein, Eric W. "Antiprism" . MathWorld .
- Prismas y antiprismas no convexos
- Modelos en papel de prismas y antiprismas.



