hipótesis de Riemann
En matemáticas, la hipótesis de Riemann es una conjetura de que la función zeta de Riemann tiene sus ceros solo en los números enteros pares negativos y los números complejos con parte real 1/2 . Muchos lo consideran el problema sin resolver más importante de las matemáticas puras . [1] Es de gran interés en teoría de números porque implica resultados sobre la distribución de los números primos . Fue propuesto por Bernhard Riemann ( 1859 ), de quien toma su nombre.
La hipótesis de Riemann y algunas de sus generalizaciones, junto con la conjetura de Goldbach y la conjetura de los primos gemelos , conforman el octavo problema de Hilbert en la lista de 23 problemas sin resolver de David Hilbert ; también es uno de los Problemas del Premio del Milenio del Clay Mathematics Institute , que ofrece un millón de dólares a quien los resuelva. El nombre también se usa para algunos análogos estrechamente relacionados, como la hipótesis de Riemann para curvas sobre campos finitos .
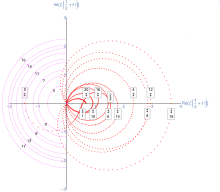
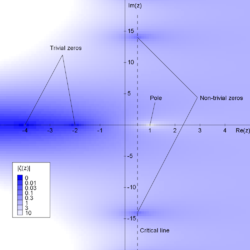
La función zeta de Riemann ζ( s ) es una función cuyo argumento s puede ser cualquier número complejo distinto de 1, y cuyos valores también son complejos. Tiene ceros en los enteros pares negativos; es decir, ζ( s ) = 0 cuando s es uno de −2, −4, −6, .... Estos se llaman sus ceros triviales . La función zeta también es cero para otros valores de s , que se denominan ceros no triviales . La hipótesis de Riemann se ocupa de las ubicaciones de estos ceros no triviales y establece que:
Por lo tanto, si la hipótesis es correcta, todos los ceros no triviales se encuentran en la línea crítica que consta de los números complejos 1/2 + i t , donde t es un número real e i es la unidad imaginaria .
La función zeta de Riemann se define para s complejos con parte real mayor que 1 por la serie infinita absolutamente convergente
Leonhard Euler ya consideró esta serie en la década de 1730 para valores reales de s, junto con su solución al problema de Basilea . También demostró que es igual al producto de Euler