Cuboctaedro
De Wikipedia, la enciclopedia libre
  (Redirigido del gráfico cuboctaédrico )
Saltar a navegación Saltar a búsqueda
Cuboctaedro
Cuboctaedro.jpg
(Haga clic aquí para ver el modelo giratorio)
EscribePoliedro uniforme sólido de Arquímedes
ElementosF = 14, E = 24, V = 12 (χ = 2)
Caras por lados8 {3} +6 {4}
Notación de ConwayaC
aaT
Símbolos de Schläflir {4,3} o rr {3,3} o
t 1 {4,3} o t 0,2 {3,3}
Símbolo de Wythoff2 | 3 4
3 3 | 2
Diagrama de CoxeterCDel node.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngCDel node.png o Nodo CDel 1.pngCDel split1-43.pngCDel nodes.png
Nodo CDel 1.pngCDel 3.pngCDel node.pngCDel 3.pngNodo CDel 1.png o CDel node.pngCDel split1.pngNodos CDel 11.png
Grupo de simetríaO h , B 3 , [4,3], (* 432), orden 48
T d , [3,3], (* 332), orden 24
Grupo de rotacionO , [4,3] + , (432), orden 24
Ángulo diedro125,26 ° segundos de
arco (- √ 3 )
ReferenciasU 07 , C 19 , W 11
PropiedadesSemiregular convexa quasiregular
Poliedro 6-8 max.png
Caras coloreadas		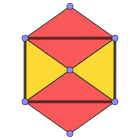Poliedro 6-8 vertfig.svg
3.4.3.4
( figura de vértice )
Poliedro 6-8 dual max.png
Dodecaedro rómbico
( poliedro dual )		Poliedro 6-8 net.svg
Neto
Modelo 3D de un cuboctaedro

Un cuboctaedro es un poliedro con 8 caras triangulares y 6 caras cuadradas. Un cuboctaedro tiene 12 vértices idénticos , con 2 triángulos y 2 cuadrados que se encuentran en cada uno, y 24 bordes idénticos , cada uno separando un triángulo de un cuadrado. Como tal, es un poliedro cuasirregular , es decir, un sólido de Arquímedes que no solo es transitivo en el vértice, sino también en el borde transitivo . Es el único poliedro convexo radialmente equilátero .

Su poliedro dual es el dodecaedro rómbico .

Platón probablemente conocía el cuboctaedro : las Definiciones de Heron cita a Arquímedes diciendo que Platón conocía un sólido formado por 8 triángulos y 6 cuadrados. [1]

Otros nombres

  • Heptaparalleloedro ( Buckminster Fuller )
    • Fuller aplicó el nombre " Dymaxion " a esta forma, utilizada en una versión anterior del mapa Dymaxion . También lo llamó "Equilibrio vectorial" debido a su simetría radial equilátera (su radio de centro a vértice es igual a la longitud de su borde). [2] Llamó a un cuboctaedro que consta de puntales rígidos conectados por vértices flexibles un "jitterbug" (esta forma se puede deformar progresivamente en un icosaedro , octaedro y tetraedro colapsando sus lados cuadrados).
  • Con O h simetría, orden 48, es un rectificada cubo o octaedro rectificado ( Norman Johnson )
  • Con T d simetría, orden 24, es un cantellated tetraedro o rhombitetratetrahedron.
  • Con simetría D 3d , orden 12, es una girobicúpula triangular .

Área y volumen

El área A y el volumen V del cuboctaedro de longitud de borde a son:

Proyecciones ortogonales

El cuboctaedro tiene cuatro proyecciones ortogonales especiales , centradas en un vértice, un borde y los dos tipos de caras, triangular y cuadrada. Los dos últimos corresponden a los planos Coxeter B 2 y A 2 . Las proyecciones sesgadas muestran un cuadrado y un hexágono que pasan por el centro del cuboctaedro.

Cuboctaedro (proyecciones ortogonales)

Cara cuadrada
Cara triangular		VérticeBordeSesgar
[4][6][2][2]
Dodecaedro rómbico (poliedro dual)

Baldosas esféricas

El cuboctaedro también puede representarse como un mosaico esférico y proyectarse sobre el plano mediante una proyección estereográfica . Esta proyección es conforme , conservando ángulos pero no áreas ni longitudes. Las líneas rectas en la esfera se proyectan como arcos circulares en el plano.

proyección ortográficacentrado en el cuadradocentrado en trianguloCentrado en vértice
Proyección estereográfica

Coordenadas cartesianas

Las coordenadas cartesianas para los vértices de un cuboctaedro (de longitud de borde √ 2 ) centradas en el origen son:

(± 1, ± 1,0)
(± 1,0, ± 1)
(0, ± 1, ± 1)

Se puede hacer un conjunto alternativo de coordenadas en 4 espacios, como 12 permutaciones de:

(0,1,1,2)

Esta construcción existe como una de las 16 facetas ortopédicas de las 16 celdas canteladas .

Vectores de raiz

Los 12 vértices del cuboctaedro pueden representar los vectores raíz del grupo de Lie simple A 3 . Con la adición de 6 vértices del octaedro , estos vértices representan los 18 vectores raíz del grupo de Lie simple B 3 .

Disección

El cuboctaedro se puede disecar en dos cúpulas triangulares mediante un hexágono común que pasa por el centro del cuboctaedro. Si estas dos cúpulas triangulares están torcidas de modo que los triángulos y los cuadrados se alineen , se crea el sólido J 27 de Johnson , la ortobicúpula triangular .

El cuboctaedro también se puede disecar en 6 pirámides cuadradas y 8 tetraedros reunidos en un punto central. Esta disección se expresa en el panal cúbico alternado donde los pares de pirámides cuadradas se combinan en octaedros .

Relaciones geométricas

Progresión entre un tetraedro , expandido en un cuboctaedro y expansión inversa en el tetraedro dual

Simetrías

Progresiones entre un octaedro , un pseudoicosaedro y un cuboctaedro

El cuboctaedro es el poliedro convexo único en el que el radio largo (de centro a vértice) es el mismo que la longitud del borde; por tanto, su diámetro largo (vértice a vértice opuesto) es de 2 longitudes de borde. Esta simetría equilátera radial es una propiedad de solo unos pocos politopos uniformes , incluido el hexágono bidimensional , el cuboctaedro tridimensional y el tesseracto de 24 y 8 celdas en cuatro dimensiones . Radialmente equiláteroLos politopos son aquellos que pueden construirse, con sus radios largos, a partir de triángulos equiláteros que se encuentran en el centro del politopo, aportando cada uno dos radios y un borde. Por tanto, todos los elementos interiores que se encuentran en el centro de estos politopos tienen caras interiores de triángulos equiláteros, como en la disección del cuboctaedro en 6 pirámides cuadradas y 8 tetraedros. Cada uno de estos politopos radialmente equiláteros también se presenta como células de un mosaico característico que llena el espacio : el mosaico de hexágonos regulares, el panal cúbico rectificado (de cuboctaedros y octaedros alternos), el panal de 24 celdas y el panal teseractico , respectivamente. Cada teselación tiene una teselación dual; los centros de celda en una teselación son vértices de celda en su teselación dual. El empaquetamiento de esferas regular más denso conocido en dos, tres y cuatro dimensiones utiliza los centros de celda de una de estas teselaciones como centros de esfera.

Un cuboctaedro tiene simetría octaédrica. Su primera estelación es el compuesto de un cubo y su octaedro dual , con los vértices del cuboctaedro ubicados en los puntos medios de los bordes de ambos.

Construcciones

Se puede obtener un cuboctaedro tomando una sección transversal ecuatorial de una celda de 24 o 16 celdas de cuatro dimensiones . Se puede obtener un hexágono tomando una sección transversal ecuatorial de un cuboctaedro.

El cuboctaedro es un cubo rectificado y también un octaedro rectificado .

También es un tetraedro cantelado . Con esta construcción se le da el símbolo de Wythoff : 3 3 | 2 .

Una cantelación sesgada del tetraedro produce un sólido con caras paralelas a las del cuboctaedro, a saber, ocho triángulos de dos tamaños y seis rectángulos. Si bien sus bordes son desiguales, este sólido permanece uniforme en los vértices : el sólido tiene el grupo de simetría tetraédrico completo y sus vértices son equivalentes en ese grupo.

Los bordes de un cuboctaedro forman cuatro hexágonos regulares . Si el cuboctaedro se corta en el plano de uno de estos hexágonos, cada mitad es una cúpula triangular , uno de los sólidos de Johnson ; el propio cuboctaedro, por tanto, también puede denominarse girobicúpula triangular , la más simple de una serie (distinta del gyrobifastigium o "gyrobicupola digonal"). Si las mitades se vuelven a unir con un giro, de modo que los triángulos se encuentran con los triángulos y los cuadrados se encuentran con los cuadrados, el resultado es otro sólido de Johnson, la ortobicúpula triangular , también llamada anticuboctaedro.

Ambas bicupolas triangulares son importantes en el empaquetamiento de esferas . La distancia desde el centro del sólido a sus vértices es igual a la longitud de su borde. Cada esfera central puede tener hasta doce vecinos, y en una celosía cúbica centrada en las caras, estos toman las posiciones de los vértices de un cuboctaedro. En una celosía hexagonal compacta, corresponden a las esquinas de la ortobicúpula triangular. En ambos casos, la esfera central toma la posición del centro del sólido.

Los cuboctaedros aparecen como células en tres de los panales uniformes convexos y en nueve de los 4 politopos uniformes convexos .

El volumen de la cuboctaedro es 5 / 6 de la del cubo circundante y 5 / 8 de la del octaedro envolvente.

Disposición de vértice

Debido a que es radialmente equilátero, el centro del cuboctaedro puede tratarse como un decimotercer vértice apical canónico , una longitud de borde distante de los 12 vértices ordinarios, ya que el vértice de una pirámide canónica es una longitud de borde equidistante de sus otros vértices.

El cuboctaedro comparte sus aristas y disposición de vértices con dos poliedros uniformes no convexos : el cubohemioctaedro (que tiene las caras cuadradas en común) y el octahemioctaedro (que tiene las caras triangulares en común), ambos tienen cuatro hexágonos. También sirve como un cantellated tetraedro , como un rectificada tetratetrahedron .


Cuboctaedro
su ecuador
Cubohemioctaedro
Octahemioctaedro

El cuboctaedro 2-cubre el tetrahemihexaedro , [3] que en consecuencia tiene la misma figura abstracta de vértice (dos triángulos y dos cuadrados: 3.4.3.4) y la mitad de los vértices, aristas y caras. (La figura vértice real de la tetrahemihexahedron es de 3.4. 3 / 2 0.4, con el un / 2 factor de debido a la cruz.)


Cuboctaedro
Tetrahemihexaedro

Poliedros relacionados

El cuboctaedro pertenece a una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Poliedros octaédricos uniformes
Simetría : [4,3], (* 432)[4,3] +
(432)		[1 + , 4,3] = [3,3]
(* 332)		[3 + , 4]
(3 * 2)
{4,3}t {4,3}r {4,3}
r {3 1,1 }		t {3,4}
t {3 1,1 }		{3,4}
{3 1,1 }		rr {4,3}
s 2 {3,4}		tr {4,3}sr {4,3}h {4,3}
{3,3}		h 2 {4,3}
t {3,3}		s {3,4}
s {3 1,1 }
Nodo CDel 1.pngCDel 4.pngCDel node.pngCDel 3.pngCDel node.pngNodo CDel 1.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngCDel node.pngCDel node.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngCDel node.pngCDel node.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.pngCDel node.pngCDel 4.pngCDel node.pngCDel 3.pngNodo CDel 1.pngNodo CDel 1.pngCDel 4.pngCDel node.pngCDel 3.pngNodo CDel 1.pngNodo CDel 1.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.pngCDel nodo h.pngCDel 4.pngCDel nodo h.pngCDel 3.pngCDel nodo h.pngCDel nodo h.pngCDel 3.pngCDel nodo h.pngCDel 4.pngCDel node.png
CDel nodo h0.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngCDel node.png
= Nodos CDel 11.pngCDel split2.pngCDel node.png		CDel nodo h0.pngCDel 4.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.png
= Nodos CDel 11.pngCDel split2.pngNodo CDel 1.png		CDel nodo h0.pngCDel 4.pngCDel node.pngCDel 3.pngNodo CDel 1.png
= CDel nodes.pngCDel split2.pngNodo CDel 1.png		Nodo CDel 1.pngCDel 4.pngCDel nodo h.pngCDel 3.pngCDel nodo h.pngNodo CDel h1.pngCDel 4.pngCDel node.pngCDel 3.pngCDel node.png =
Nodos CDel 10ru.pngCDel split2.pngCDel node.png o Nodos CDel 01rd.pngCDel split2.pngCDel node.png		Nodo CDel h1.pngCDel 4.pngCDel node.pngCDel 3.pngNodo CDel 1.png =
Nodos CDel 10ru.pngCDel split2.pngNodo CDel 1.png o Nodos CDel 01rd.pngCDel split2.pngNodo CDel 1.png		CDel nodo h.pngCDel 3.pngCDel nodo h.pngCDel 4.pngCDel nodo h0.png =
CDel nodo h.pngCDel split1.pngNodos CDel hh.png





Poliedros duales a uniformes
V4 3V3.8 2V (3,4) 2V4.6 2V3 4V3.4 3V4.6.8V3 4 .4V3 3V3.6 2V3 5
CDel nodo f1.pngCDel 4.pngCDel node.pngCDel 3.pngCDel node.pngCDel nodo f1.pngCDel 4.pngCDel nodo f1.pngCDel 3.pngCDel node.pngCDel node.pngCDel 4.pngCDel nodo f1.pngCDel 3.pngCDel node.pngCDel node.pngCDel 4.pngCDel nodo f1.pngCDel 3.pngCDel nodo f1.pngCDel node.pngCDel 4.pngCDel node.pngCDel 3.pngCDel nodo f1.pngCDel nodo f1.pngCDel 4.pngCDel node.pngCDel 3.pngCDel nodo f1.pngCDel nodo f1.pngCDel 4.pngCDel nodo f1.pngCDel 3.pngCDel nodo f1.pngCDel nodo fh.pngCDel 4.pngCDel nodo fh.pngCDel 3.pngCDel nodo fh.pngCDel nodo fh.pngCDel 4.pngCDel node.pngCDel 3.pngCDel node.pngCDel nodo fh.pngCDel 4.pngCDel node.pngCDel 3.pngCDel nodo f1.pngCDel nodo fh.pngCDel 3.pngCDel nodo fh.pngCDel 4.pngCDel node.png
CDel nodo f1.pngCDel 3.pngCDel node.pngCDel 3.pngCDel nodo f1.pngCDel nodo f1.pngCDel 3.pngCDel nodo f1.pngCDel 3.pngCDel nodo f1.pngCDel node.pngCDel 3.pngCDel nodo f1.pngCDel 3.pngCDel node.pngCDel nodo f1.pngCDel 4.pngCDel nodo fh.pngCDel 3.pngCDel nodo fh.pngCDel nodo f1.pngCDel 3.pngCDel node.pngCDel 3.pngCDel node.pngCDel node.pngCDel 3.pngCDel nodo f1.pngCDel 3.pngCDel nodo f1.pngCDel nodo fh.pngCDel 3.pngCDel nodo fh.pngCDel 3.pngCDel nodo fh.png

El cuboctaedro también tiene simetría tetraédrica con dos colores de triángulos.

Familia de poliedros tetraédricos uniformes
Simetría : [3,3] , (* 332)[3,3] + , (332)
Nodo CDel 1.pngCDel 3.pngCDel node.pngCDel 3.pngCDel node.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.pngCDel 3.pngCDel node.pngCDel node.pngCDel 3.pngNodo CDel 1.pngCDel 3.pngCDel node.pngCDel node.pngCDel 3.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.pngCDel node.pngCDel 3.pngCDel node.pngCDel 3.pngNodo CDel 1.pngNodo CDel 1.pngCDel 3.pngCDel node.pngCDel 3.pngNodo CDel 1.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.pngCDel 3.pngNodo CDel 1.pngCDel nodo h.pngCDel 3.pngCDel nodo h.pngCDel 3.pngCDel nodo h.png
{3,3}t {3,3}r {3,3}t {3,3}{3,3}rr {3,3}tr {3,3}sr {3,3}
Poliedros duales a uniformes
V3.3.3V3.6.6V3.3.3.3V3.6.6V3.3.3V3.4.3.4V4.6.6V3.3.3.3.3

Poliedros y teselados cuasirregulares relacionados

El cuboctaedro existe en una secuencia de simetrías de poliedros cuasirregulares y mosaicos con configuraciones de vértice (3. n ) 2 , progresando desde los mosaicos de la esfera al plano euclidiano y al plano hiperbólico. Con la simetría de notación orbifold de * n 32, todos estos mosaicos son construcciones de wythoff dentro de un dominio fundamental de simetría, con puntos generadores en la esquina del ángulo recto del dominio. [4] [5]

* n 32 simetrías orbifold de teselaciones cuasirregulares : (3. n ) 2

Construcción		EsféricoEuclidianaHiperbólico
* 332* 432* 532* 632* 732* 832 ...* ∞32

Figuras cuasirregulares
Vértice(3.3) 2(3.4) 2(3,5) 2(3,6) 2(3,7) 2(3,8) 2(3.∞) 2
* n 42 mutaciones de simetría de teselaciones cuasirregulares: (4. n ) 2
  • v
  • t
  • mi
Simetría
* 4 n 2
[n, 4]		EsféricoEuclidianaHiperbólico compactoParacompactoNo compacto
* 342
[3,4]		* 442
[4,4]		* 542
[5,4]		* 642
[6,4]		* 742
[7,4]		* 842
[8,4] ...		* ∞42
[∞, 4]		 
[ n i, 4]
Cifras
Config.(4,3) 2(4,4) 2(4,5) 2(4,6) 2(4,7) 2(4,8) 2(4.∞) 2(4. n i) 2

Este poliedro está relacionada topológicamente con como una parte de la secuencia de cantellated poliedros con la figura vértice (3.4. N 0.4), y continúa como embaldosados del plano hiperbólico . Estas figuras transitivas de vértice tienen (* n 32) simetría de reflexión .

* n 32 mutación de simetría de teselaciones expandidas: 3.4. n. 4
Simetría
* n 32
[n, 3]		EsféricoEuclides.Hyperb compacto.Paracomp.
* 232
[2,3]		* 332
[3,3]		* 432
[4,3]		* 532
[5,3]		* 632
[6,3]		* 732
[7,3]		* 832
[8,3] ...		* ∞32
[∞, 3]
Figura
Config.3.4.2.43.4.3.43.4.4.43.4.5.43.4.6.43.4.7.43.4.8.43.4.∞.4

Politopos relacionados

Proyecciones ortogonales de 24 celdas

El cuboctaedro se puede descomponer en un octaedro regular y ocho octaedros irregulares pero iguales en la forma del casco convexo de un cubo con dos vértices opuestos eliminados. Esta descomposición del cuboctaedro se corresponde con la proyección paralela de la primera celda de las 24 celdas en tres dimensiones. Bajo esta proyección, el cuboctaedro forma la envolvente de la proyección, que se puede descomponer en seis caras cuadradas, un octaedro regular y ocho octaedros irregulares. Estos elementos se corresponden con las imágenes de seis de las celdas octaédricas en las 24 celdas, las celdas más cercanas y más lejanas desde el punto de vista 4D y los ocho pares de celdas restantes, respectivamente.

Acontecimientos culturales

Dos cuboctaedros en una chimenea en Israel .
  • En el episodio de Star Trek " Por cualquier otro nombre ", los extraterrestres se apoderan de la Enterprise transformando a los miembros de la tripulación en cuboctaedros inanimados.
  • El juguete inquietante "Geo Twister" [1] es un cuboctaedro flexible.
  • Las estaciones espaciales Coriolis de la serie de juegos de computadora Elite tienen forma de cuboctaedro.
  • Vesak Kuudu, linternas tradicionales que se fabrican anualmente en Sri Lanka para celebrar el día de Vesak Poya, suelen ser cuboctaédricas.
  • "Moonsnakes" de Super Mario Odyssey . [6]
  • InfluxData , la empresa detrás de la base de datos de series de tiempo de InfluxDB , utiliza el cuboctaedro en su logotipo .

Gráfico cuboctaédrico

Gráfico cuboctaédrico
Simetría cuádruple
Vértices12
Bordes24
Automorfismos48
Propiedades
  • Cuartico
  • Hamiltoniano
  • regular
  • localmente lineal
Tabla de gráficos y parámetros

En el campo matemático de la teoría de grafos , un gráfico cuboctaédrico es el gráfico de vértices y aristas del cuboctaedro, uno de los sólidos de Arquímedes . También se puede construir como la gráfica lineal del cubo. Tiene 12 vértices y 24 bordes, es localmente lineal , y es un quartic gráfico de Arquímedes . [7]

proyección ortogonal

Simetría de 6 pliegues

Ver también

  • Icosidodecaedro
  • Pseudocuboctaedro
  • Rombicuboctaedro
  • Cuboctaedro truncado
  • Tetradecaedro

Referencias

  1. ^ Heath, Thomas L. (1931), "Un manual de matemáticas griegas", Nature , Clarendon, 128 (3235): 739–740, Bibcode : 1931Natur.128..739T , doi : 10.1038 / 128739a0 , S2CID  3994109
  2. ^ Equilibrio vectorial: R. Buckminster Fuller
  3. ^ Richter, David A., dos modelos de la proyectiva real Plano , Archivado desde el original en 03/03/2016 , recuperado 2010-04-15
  4. ^ Coxeter, HSM (1973), Politopos regulares (3.a ed.), Dover, Capítulo V: El caleidoscopio, Sección: 5.7 Construcción de Wythoff , ISBN 0-486-61480-8
  5. ^ Mutaciones de simetría bidimensional por Daniel Huson
  6. ^ "Archivo: Moonsnake Icon SMO.png - Super Mario Wiki, la enciclopedia de Mario" . www.mariowiki.com . Consultado el 5 de noviembre de 2018 .
  7. ^ Leer, RC; Wilson, RJ (1998), An Atlas of Graphs , Oxford University Press , pág. 269

Otras lecturas

  • Ghyka, Matila (1977). La geometría del arte y la vida ([Nachdr.] Ed.). Nueva York: Publicaciones de Dover . págs.  51–56, 81–84 . ISBN 9780486235424.
  • Weisstein, Eric W. (2002). "Cuboctaedro". Enciclopedia Concisa de Matemáticas CRC (2ª ed.). Hoboken: CRC Press . págs. 620–621. ISBN 9781420035223.
  • Williams, Robert (1979). La base geométrica de la estructura natural: un libro fuente de diseño . Publicaciones de Dover, Inc. ISBN 0-486-23729-X. (Sección 3-9)
  • Cromwell, P. Polyhedra , CUP hbk (1997), pbk. (1999). Capítulo 2 p. 79-86 sólidos de Arquímedes

enlaces externos

  • Los poliedros uniformes
  • Poliedros de realidad virtual La enciclopedia de poliedros
  • Eric W. Weisstein , Cuboctahedron ( sólido de Arquímedes ) en MathWorld .
  • El Cuboctaedro en Hexnet, un sitio web dedicado a las matemáticas hexagonales.
  • Klitzing, Richard. "Poliedros uniformes convexos 3D o3x4o - co" .
  • Red imprimible editable de un Cuboctaedro con vista 3D interactiva
Obtenido de " https://en.wikipedia.org/w/index.php?title=Cuboctahedron&oldid=1049491094#Cuboctahedral_graph "
Contribute a better translation