Mosaicos euclidianos por polígonos regulares convexos

Ejemplo de teselaciones periódicas

Un mosaico regular tiene un tipo de cara regular.	Un mosaico semirregular o uniforme tiene un tipo de vértice , pero dos o más tipos de caras.
Un mosaico k -uniforme tiene k tipos de vértices y dos o más tipos de caras regulares.	Un mosaico que no es de borde a borde puede tener caras regulares de diferentes tamaños.

Los mosaicos planos euclidianos por polígonos regulares convexos se han utilizado ampliamente desde la antigüedad. El primer tratamiento matemático sistemático fue el de Kepler en sus Harmonices Mundi ( Latín : The Harmony of the World , 1619).

Azulejos regulares

Siguiendo a Grünbaum y Shephard (sección 1.3), se dice que un mosaico es regular si el grupo de simetría del mosaico actúa de manera transitiva sobre las banderas del mosaico, donde una bandera es un triple que consiste en un vértice , borde y mosaico mutuamente incidentes de la embaldosado. Esto significa que, para cada par de banderas, hay una operación de simetría que asigna la primera bandera a la segunda. Esto es equivalente a que el mosaico sea un mosaico de borde a borde mediante polígonos regulares congruentes . Debe haber seis triángulos equiláteros , cuatro cuadrados o tres hexágonos regularesen un vértice, produciendo las tres teselaciones regulares .

Azulejos regulares (3)

p6m, * 632		p4m, * 442
3 6 (t = 1, e = 1)	6 3 (t = 1, e = 1)	4 4 (t = 1, e = 1)

Azulejos de Arquímedes, uniformes o semirregulares

Transitividad de vértice significa que para cada par de vértices hay una operación de simetría que mapea el primer vértice con el segundo. ^[1]

Si el requisito de la bandera-transitividad se relaja a uno de vértice-transitividad, mientras se mantiene la condición de que el mosaico sea de borde a borde, hay ocho mosaicos adicionales posibles, conocidos como mosaicos de Arquímedes , uniformes o semirregulares . Tenga en cuenta que hay dos formas de imagen especular (enantiomórfica o quiral ) de mosaico 3 ⁴ .6 (hexagonal chato), de las cuales solo se muestra una en la siguiente tabla. Todos los demás revestimientos regulares y semirregulares son aquirales.

Azulejos uniformes (8)

p6m, * 632
3.12 2 (t = 2, e = 2) t {6,3}	3.4.6.4 (t = 3, e = 2) rr {3,6}	4.6.12 (t = 3, e = 3) tr {3,6}	(3.6) 2 (t = 2, e = 1) r {6,3}
4.8 2 (t = 2, e = 2) t {4,4}	3 2 .4.3.4 (t = 2, e = 2) s {4,4}	3 3 .4 2 (t = 2, e = 3) {3,6}: e	3 4 .6 (t = 3, e = 3) sr {3,6}

Grünbaum y Shephard distinguen la descripción de estos mosaicos como Arquímedes como una referencia solo a la propiedad local de que la disposición de los mosaicos alrededor de cada vértice es la misma, y ​​que es tan uniforme como una referencia a la propiedad global de la transitividad del vértice. Aunque estos producen el mismo conjunto de mosaicos en el plano, en otros espacios hay mosaicos de Arquímedes que no son uniformes.

k -cosas uniformes

3-baldosas uniformes # 57 de 61 de colores

por lados, triángulos amarillos, cuadrados rojos (por polígonos)

por 4 posiciones isoédricas, 3 colores sombreados de triángulos (por órbitas)

Estos mosaicos periódicos pueden clasificarse por el número de órbitas de vértices, bordes y mosaicos. Si hay k órbitas de vértices, un mosaico se conoce como k -uniforme o k -isogonal; si hay t órbitas de mosaicos, como t -isoédrico; si hay e órbitas de aristas, como e -isotoxal.

k -los mosaicos uniformes con las mismas figuras de vértice pueden identificarse aún más por su simetría de grupo de papel tapiz .

Los mosaicos 1-uniformes incluyen 3 mosaicos regulares y 8 semirregulares, con 2 o más tipos de caras poligonales regulares. Hay 20 mosaicos uniformes 2, 61 mosaicos uniformes 3, 151 mosaicos uniformes 4, 332 mosaicos uniformes 5 y 673 mosaicos uniformes 6. Cada uno se puede agrupar por el número m de distintas figuras de vértice, que también se denominan m - mosaicos arquimedianos. ^[2]

Finalmente, si el número de tipos de vértices es el mismo que la uniformidad ( m = k abajo), entonces se dice que el mosaico es Krotenheerdt . En general, la uniformidad es mayor o igual al número de tipos de vértices ( m ≥ k ), ya que diferentes tipos de vértices necesariamente tienen diferentes órbitas, pero no al revés. Configurando m = n = k , hay 11 teselaciones de este tipo para n = 1; 20 de tales teselaciones para n = 2; 39 tales teselaciones para n = 3; 33 de tales teselaciones para n = 4; 15 de tales teselaciones para n = 5; 10 tales cosas paran = 6; y 7 de tales teselaciones para n = 7.

k -uniforme, m -Archimedean Tiling count ^[3]

		m -Archimedean
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	≥ 15	Total
k -uniforme	1	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	11
	2	0	20	0	0	0	0	0	0	0	0	0	0	0	0	0	20
	3	0	22	39	0	0	0	0	0	0	0	0	0	0	0	0	61
	4	0	33	85	33	0	0	0	0	0	0	0	0	0	0	0	151
	5	0	74	149	94	15	0	0	0	0	0	0	0	0	0	0	332
	6	0	100	284	187	92	10	0	0	0	0	0	0	0	0	0	673
	7	0	?	?	?	?	?	7	0	0	0	0	0	0	0	0	?
	8	0	?	?	?	?	?	20	0	0	0	0	0	0	0	0	?
	9	0	?	?	?	?	?	?	8	0	0	0	0	0	0	0	?
	10	0	?	?	?	?	?	?	27	0	0	0	0	0	0	0	?
	11	0	?	?	?	?	?	?	?	1	0	0	0	0	0	0	?
	12	0	?	?	?	?	?	?	?	?	0	0	0	0	0	0	?
	13	0	?	?	?	?	?	?	?	?	?	?	?	0	0	0	?
	14	0	?	?	?	?	?	?	?	?	?	?	?	?	0	0	?
	≥ 15	0	?	?	?	?	?	?	?	?	?	?	?	?	?	0	?
	Total	11	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	0	∞

Polígonos regulares disecados

Algunas de las teselaciones uniformes k se pueden derivar diseccionando simétricamente los polígonos de teselación con bordes interiores, por ejemplo (disección directa):

Polígonos disecados con bordes originales

Hexágono	Dodecágono (cada uno tiene 2 orientaciones)

Algunas teselaciones k-uniformes se pueden derivar diseccionando polígonos regulares con nuevos vértices a lo largo de los bordes originales, por ejemplo (disección indirecta):

Diseccionado con 1 o 2 vértices medios

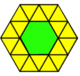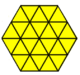Triángulo			Cuadrado		Hexágono

Finalmente, para ver todos los tipos de configuraciones de vértices, consulte Planigon .

2-mosaicos uniformes

Hay veinte (20) mosaicos 2 uniformes del plano euclidiano. (también llamados mosaicos 2- isogonales o mosaicos semirregulares ) ^{[4] [5] [6] Los} tipos de vértice se enumeran para cada uno. Si dos teselaciones comparten los mismos dos tipos de vértices, se les asignan subíndices 1,2.

2-mosaicos uniformes (20)

p6m, * 632						p4m, * 442
[3 6 ; 3 2 .4.3.4] (t = 3, e = 3)	[3.4.6.4; 3 2 .4.3.4] (t = 4, e = 4)	[3.4.6.4; 3 3 .4 2 ] (t = 4, e = 4)	[3.4.6.4; 3.4 2 .6] (t = 5, e = 5)	[4.6.12; 3.4.6.4] (t = 4, e = 4)	[3 6 ; 3 2 .4.12] (t = 4, e = 4)	[3.12.12; 3.4.3.12] (t = 3, e = 3)
p6m, * 632	p6, 632	p6, 632	cmm, 2 * 22	mmm, * 2222	cmm, 2 * 22	mmm, * 2222
[3 6 ; 3 2 .6 2 ] (t = 2, e = 3)	[3 6 ; 3 4 .6] 1 (t = 3, e = 3)	[3 6 ; 3 4 .6] 2 (t = 5, e = 7)	[3 2 .6 2 ; 3 4 .6] (t = 2, e = 4)	[3.6.3.6; 3 2 .6 2 ] (t = 2, e = 3)	[3.4 2 .6; 3.6.3.6] 2 (t = 3, e = 4)	[3.4 2 .6; 3.6.3.6] 1 (t = 4, e = 4)
p4g, 4 * 2	pgg, 22 ×	cmm, 2 * 22	cmm, 2 * 22	mmm, * 2222	cmm, 2 * 22
[3 3 .4 2 ; 3 2 .4.3.4] 1 (t = 4, e = 5)	[3 3 .4 2 ; 3 2 .4.3.4] 2 (t = 3, e = 6)	[4 4 ; 3 3 .4 2 ] 1 (t = 2, e = 4)	[4 4 ; 3 3 .4 2 ] 2 (t = 3, e = 5)	[3 6 ; 3 3 .4 2 ] 1 (t = 3, e = 4)	[3 6 ; 3 3 .4 2 ] 2 (t = 4, e = 5)

Azulejos k-uniformes superiores

k -mosaicos uniformes se han enumerado hasta 6. Hay 673 mosaicos 6-uniformes del plano euclidiano. La búsqueda de Brian Galebach reprodujo la lista de Krotenheerdt de 10 mosaicos uniformes de 6 con 6 tipos de vértices distintos, además de encontrar 92 de ellos con 5 tipos de vértices, 187 de ellos con 4 tipos de vértices, 284 de ellos con 3 tipos de vértices y 100 con 2 tipos de vértice.

Fractalizar teselas del uniforme k

Hay muchas formas de generar nuevos mosaicos de uniforme k a partir de mosaicos de uniforme k antiguos. Por ejemplo, observe que el 2-uniforme [3.12.12; 3.4.3.12] el mosaico tiene una celosía cuadrada, el 4 (3-1) -uniforme [343.12; (3.12 ² ) 3] el embaldosado tiene una celosía cuadrada chata, y el 5 (3-1-1) -uniforme [334.12; 343,12; (3.12.12) 3] las baldosas tienen una celosía triangular alargada. Estos mosaicos uniformes de orden superior utilizan la misma celosía pero poseen una mayor complejidad. La base de fractalización de estas teselaciones es la siguiente: ^[7]

	Triángulo	Cuadrado	Hexágono	Dodecágono disecado
Forma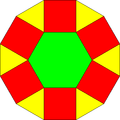
Fractalizando

Las longitudes de los lados están dilatadas por un factor de ${\displaystyle 2+{\sqrt {3}}}$.

Esto se puede hacer de manera similar con el mosaico trihexagonal truncado como base, con la correspondiente dilatación de ${\displaystyle 3+{\sqrt {3}}}$.

	Triángulo	Cuadrado	Hexágono	Dodecágono disecado
Forma
Fractalizando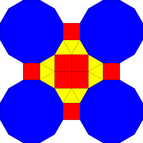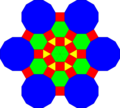

Ejemplos de fractalización

	Mosaico hexagonal truncado	Azulejos truncados trihexagonales
Fractalizando

Azulejos que no son de borde a borde

Los polígonos regulares convexos también pueden formar mosaicos planos que no son de borde a borde. Estos mosaicos pueden considerarse de borde a borde como polígonos no regulares con bordes colineales adyacentes.

Hay siete familias de isogonales, cada una de las cuales tiene un parámetro de valor real que determina la superposición entre los lados de las baldosas adyacentes o la relación entre las longitudes de los bordes de las diferentes baldosas. Dos de las familias se generan a partir del cuadrado desplazado, ya sea en posición progresiva o en zigzag. Grünbaum y Shephard llaman a estos mosaicos uniformes, aunque contradice la definición de Coxeter de uniformidad que requiere polígonos regulares de borde a borde. ^[8] Estos mosaicos isogonales son en realidad topológicamente idénticos a los mosaicos uniformes, con diferentes proporciones geométricas.

Mosaicos isogonales periódicos por polígonos regulares convexos que no son de borde a borde

1	2	3	4	5	6	7
Filas de cuadrados con desplazamientos horizontales		Filas de triángulos con desplazamientos horizontales	Un mosaico por cuadrados	Tres hexágonos rodean cada triángulo	Seis triángulos rodean cada hexágono.	Triángulos de tres tamaños
cmm (2 * 22)	p2 (2222)	cmm (2 * 22)	p4m (* 442)	p6 (632)		p3 (333)
Azulejos hexagonales		Azulejos cuadrados	Azulejos cuadrados truncados	Baldosas hexagonales truncadas	Azulejos hexagonales	Azulejos trihexagonales

Ver también

• Azulejos uniformes en plano hiperbólico
• Lista de mosaicos uniformes
• Símbolo de Wythoff
• Mosaico
• Grupo de papel tapiz
• Poliedro regular (los sólidos platónicos )
• Poliedro semirregular (incluidos los sólidos de Arquímedes )
• Geometría hiperbólica
• Baldosas Penrose
• Azulejos con rectángulos
• Celosía (grupo)

Referencias

1. Critchlow, p.60-61
2. K-uniformes teselados por polígonos regulares Archivado el 30 de junio de 2015 en la Wayback Machine Nils Lenngren, 2009
3. "Azulejos n-uniformes" . probabilidadsports.com . Consultado el 21 de junio de 2019 .
4. Critchlow, p.62-67
5. Azulejos y patrones, Grünbaum y Shephard 1986, págs. 65-67
6. "En busca de mosaicos demirregulares" (PDF) . Archivado desde el original (PDF) el 7 de mayo de 2016 . Consultado el 4 de junio de 2015 .
7. Chavey, Darrah (2014). "ALICATADOS POR POLÍGONOS REGULARES III: ALICATADOS DODECAGON-DENSOS". Simetría-Cultura y Ciencia . 25 (3): 193–210. S2CID 33928615 . 
8. Mosaicos por polígonos regulares p.236

• Grünbaum, Branko; Shephard, Geoffrey C. (1977). "Tilings por polígonos regulares". Matemáticas. Mag . 50 (5): 227–247. doi : 10.2307 / 2689529 . JSTOR  2689529 .
• Grünbaum, Branko; Shephard, GC (1978). "Los noventa y un tipos de teselaciones isogonales en el plano" . Trans. Soy. Matemáticas. Soc . 252 : 335–353. doi : 10.1090 / S0002-9947-1978-0496813-3 . Señor  0496813 .
• Debroey, I .; Landuyt, F. (1981). "Alicatados equitransitivos de borde a borde". Geometriae Dedicata . 11 (1): 47–60. doi : 10.1007 / BF00183189 . S2CID  122636363 .
• Grünbaum, Branko ; Shephard, GC (1987). Azulejos y Patrones . WH Freeman and Company. ISBN 0-7167-1193-1.
• Ren, Ding; Reay, John R. (1987). "La característica de la frontera y el teorema de Pick en los mosaicos planos de Arquímedes" . J. Combinat. Una teoría . 44 (1): 110-119. doi : 10.1016 / 0097-3165 (87) 90063-X .
• Chavey, D. (1989). "Mosaicos por polígonos regulares — II: un catálogo de mosaicos" . Computadoras y Matemáticas con Aplicaciones . 17 : 147-165. doi : 10.1016 / 0898-1221 (89) 90156-9 .
• Order in Space: A design source book, Keith Critchlow, 1970 ISBN 978-0-670-52830-1 
• Sommerville, Duncan MacLaren Young (1958). Introducción a la geometría de n dimensiones . Publicaciones de Dover. Capítulo X: Los politopos regulares
• Préa, P. (1997). "Secuencias de distancia y umbrales de percolación en Azulejos de Arquímedes" . Mathl. Computación. Modelado . 26 (8-10): 317-320. doi : 10.1016 / S0895-7177 (97) 00216-1 .
• Kovic, Jurij (2011). "Gráficos de tipo simetría de sólidos platónicos y de Arquímedes" . Matemáticas. Comun . 16 (2): 491–507.
• Pellicer, Daniel; Williams, Gordon (2012). "Cubiertas mínimas de los mosaicos de Arquímedes, parte 1" . La Revista Electrónica de Combinatoria . 19 (3): # P6. doi : 10.37236 / 2512 .
• Dale Seymour y Jill Britton , Introducción a los mosaicos , 1989, ISBN 978-0866514613 , págs. 50–57 

Enlaces externos

Enlaces de mosaico euclidianos y generales:

• teselas n-uniformes , Brian Galebach
• Holandés, Steve. "Azulejos uniformes" . Archivado desde el original el 9 de septiembre de 2006 . Consultado el 9 de septiembre de 2006 .
• Mitchell, K. "Tilings semi-regulares" . Consultado el 9 de septiembre de 2006 .
• Weisstein, Eric W. "Teselación" . MathWorld .
• Weisstein, Eric W. "teselación semirregular" . MathWorld .
• Weisstein, Eric W. "teselación demirregular" . MathWorld .