Álgebra tensorial

Construcción universal en álgebra multilineal

En matemáticas , el álgebra tensorial de un espacio vectorial V , denotado T ( V ) o T ^• ( V ), es el álgebra de tensores en V (de cualquier rango) siendo la multiplicación el producto tensorial . Es el álgebra libre en V , en el sentido de estar junto al functor olvidadizo de álgebras a espacios vectoriales: es el álgebra "más general" que contiene V , en el sentido de la propiedad universal correspondiente.(ver más abajo ).

El álgebra tensorial es importante porque muchas otras álgebras surgen como álgebras cocientes de T ( V ). Estos incluyen el álgebra exterior , el álgebra simétrica , las álgebras de Clifford , el álgebra de Weyl y las álgebras envolventes universales .

El álgebra tensorial también tiene dos estructuras de coalgebra ; uno simple, que no lo convierte en una bialgebra, pero conduce al concepto de cofree coalgebra , y uno más complicado, que produce una bialgebra , y puede extenderse dando una antípoda para crear una estructura de álgebra de Hopf .

Nota : En este artículo, se supone que todas las álgebras son unitales y asociativas . Se requiere explícitamente que la unidad defina el coproducto.

Construcción

Deje que V sea un espacio vectorial sobre un campo K . Para cualquier entero no negativo k , definimos la k- ésima potencia del tensor de V como el producto tensorial de V consigo mismo k veces:

${\displaystyle T^{k}V=V^{\otimes k}=V\otimes V\otimes \cdots \otimes V.}$

Es decir, T ^k V consta de todos los tensores en V de orden k . Por convención, T ⁰ V es el campo de tierra K (como un espacio vectorial unidimensional sobre sí mismo).

Luego construimos T ( V ) como la suma directa de T ^k V para k = 0,1,2,…

${\displaystyle T(V)=\bigoplus _{k=0}^{\infty }T^{k}V=K\oplus V\oplus (V\otimes V)\oplus (V\otimes V\otimes V)\oplus \cdots .}$

La multiplicación en T ( V ) está determinada por el isomorfismo canónico

${\displaystyle T^{k}V\otimes T^{\ell }V\to T^{k+\ell }V}$

dado por el producto tensorial, que luego se extiende por linealidad a todo T ( V ). Esta regla de multiplicación implica que el álgebra tensorial T ( V ) es naturalmente un álgebra graduada con T ^k V que sirve como subespacio de grado- k . Esta calificación se puede extender a una calificación Z agregando subespacios${\displaystyle T^{k}V=\{0\}}$para enteros negativos k .

La construcción se generaliza de manera sencilla al álgebra tensorial de cualquier módulo M sobre un anillo conmutativo . Si R es un anillo no conmutativo , todavía se puede realizar la construcción para cualquier R - R bimodule M . (No funciona para módulos R ordinarios porque los productos tensoriales iterados no se pueden formar).

Adjunción y propiedad universal

El álgebra tensorial T ( V ) también se denomina álgebra libre en el espacio vectorial V y es functorial. Como ocurre con otras construcciones libres , el functor T se deja adjunto a algún functor olvidadizo . En este caso, es el funtor el que envía cada K -álgebra a su espacio vectorial subyacente.

Explícitamente, el álgebra tensorial satisface la siguiente propiedad universal , que expresa formalmente el enunciado de que es el álgebra más general que contiene V :

Cualquier transformación lineal f  : V → A de V a un álgebra A sobre K se puede extender de manera única a un homomorfismo de álgebra de T ( V ) a A como lo indica el siguiente diagrama conmutativo :

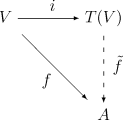
Aquí i es la inclusión canónica de V en T ( V ) (la unidad del adjunto). De hecho, se puede definir el álgebra tensorial T ( V ) como el álgebra única que satisface esta propiedad (específicamente, es única hasta un isomorfismo único), pero aún se debe demostrar que existe un objeto que satisface esta propiedad.

Los espectáculos de propiedad universales anteriores que la construcción de la álgebra del tensor es funtorial en la naturaleza. Es decir, T es un funtor de K -Vect , la categoría de espacios vectoriales sobre K , a K -Alg , la categoría de K -álgebras. La functorialidad de T significa que cualquier mapa lineal entre los espacios de K -vector U y W se extiende únicamente a un homomorfismo de K -álgebra de T ( U ) a T ( W ).

Polinomios no conmutativos

Si V tiene una dimensión finita n , otra forma de ver el álgebra tensorial es como el "álgebra de polinomios sobre K en n variables no conmutadas". Si tomamos vectores base para V , estos se convierten en variables no conmutadas (o indeterminadas ) en T ( V ), sin restricciones más allá de la asociatividad , la ley distributiva y la K- linealidad.

Tenga en cuenta que el álgebra de polinomios en V no es${\displaystyle T(V)}$, sino más bien ${\displaystyle T(V^{*})}$: una función lineal (homogénea) en V es un elemento de${\displaystyle V^{*},}$ por ejemplo coordenadas ${\displaystyle x^{1},\dots ,x^{n}}$en un espacio vectorial son covectores , ya que toman un vector y dan un escalar (la coordenada dada del vector).

Cocientes

Debido a la generalidad del álgebra tensorial, se pueden construir muchas otras álgebras de interés comenzando con el álgebra tensorial y luego imponiendo ciertas relaciones a los generadores, es decir, construyendo ciertas álgebras cocientes de T ( V ). Ejemplos de esto son el álgebra exterior , el álgebra simétrica , álgebra de Clifford , el Weyl álgebra y álgebras envolventes universales .

Coalgebra

El álgebra tensorial tiene dos estructuras de coalgebra diferentes . Uno es compatible con el producto tensorial y, por lo tanto, puede extenderse a una bialgebra , y puede extenderse aún más con una antípoda a una estructura de álgebra de Hopf . La otra estructura, aunque más simple, no se puede extender a una bialgebra. La primera estructura se desarrolla inmediatamente debajo; la segunda estructura se da en la sección sobre el cofree coalgebra , más abajo.

El desarrollo proporcionado a continuación se puede aplicar igualmente bien al álgebra exterior , utilizando el símbolo de la cuña${\displaystyle \wedge }$ en lugar del símbolo del tensor ${\displaystyle \otimes }$; también se debe realizar un seguimiento de una señal al permutar elementos del álgebra exterior. Esta correspondencia también perdura a través de la definición de la bialgebra, y hasta la definición de un álgebra de Hopf. Es decir, al álgebra exterior también se le puede dar una estructura de álgebra de Hopf.

De manera similar, al álgebra simétrica también se le puede dar la estructura de un álgebra de Hopf, exactamente de la misma manera, reemplazando en todas partes el producto tensorial${\displaystyle \otimes }$ por el producto tensorial simetrizado ${\displaystyle \otimes _{\mathrm {Sym} }}$, es decir, ese producto donde ${\displaystyle v\otimes _{\mathrm {Sym} }w=w\otimes _{\mathrm {Sym} }v.}$

En cada caso, esto es posible porque el producto alterno ${\displaystyle \wedge }$ y el producto simétrico ${\displaystyle \otimes _{\mathrm {Sym} }}$obedecer las condiciones de consistencia requeridas para la definición de una bialgebra y álgebra de Hopf; esto se puede comprobar explícitamente de la siguiente manera. Siempre que se tiene un producto que obedece a estas condiciones de consistencia, la construcción es minuciosa; en la medida en que tal producto dio lugar a un espacio de cociente, el espacio de cociente hereda la estructura del álgebra de Hopf.

En el lenguaje de la teoría de categorías , se dice que hay un functor T de la categoría de K -espacios de vectores a la categoría de K- álgebras asociadas. Pero también hay un funtor Λ que lleva los espacios vectoriales a la categoría de álgebras exteriores, y un funtor Sym que lleva los espacios vectoriales a álgebras simétricas. Hay un mapa natural de T a cada uno de estos. Verificar que el cociente conserva la estructura del álgebra de Hopf es lo mismo que verificar que los mapas son realmente naturales.

Coproducto

La coalgebra se obtiene definiendo un coproducto u operador diagonal

${\displaystyle \Delta :TV\to TV\boxtimes TV}$

Aquí, ${\displaystyle TV}$ se utiliza como una abreviatura de ${\displaystyle T(V)}$para evitar una explosión de paréntesis. El${\displaystyle \boxtimes }$El símbolo se usa para denotar el producto tensorial "externo", necesario para la definición de una coalgebra. Se utiliza para distinguirlo del producto tensorial "interno".${\displaystyle \otimes }$, que ya está "tomado" y se usa para denotar multiplicación en el álgebra tensorial (consulte la sección Multiplicación , más adelante, para obtener más aclaraciones sobre este tema). Para evitar confusiones entre estos dos símbolos, la mayoría de los textos reemplazarán${\displaystyle \otimes }$por un punto simple, o incluso elimínelo por completo, en el entendimiento de que está implícito en el contexto. Esto permite entonces que el${\displaystyle \otimes }$ símbolo que se utilizará en lugar del ${\displaystyle \boxtimes }$símbolo. Esto no se hace a continuación, y los dos símbolos se utilizan de forma independiente y explícita para mostrar la ubicación correcta de cada uno. El resultado es un poco más detallado, pero debería ser más fácil de comprender.

La definición del operador ${\displaystyle \Delta }$ se construye más fácilmente en etapas, primero definiéndolo para elementos ${\displaystyle v\in V\subset TV}$y luego extendiéndolo homomórficamente a todo el álgebra. Entonces, una elección adecuada para el coproducto es

${\displaystyle \Delta :v\mapsto v\boxtimes 1+1\boxtimes v}$

y

${\displaystyle \Delta :1\mapsto 1\boxtimes 1}$

donde ${\displaystyle 1\in K=T^{0}V\subset TV}$ es la unidad del campo ${\displaystyle K}$. Por linealidad, uno obviamente tiene

${\displaystyle \Delta (k)=k(1\boxtimes 1)=k\boxtimes 1=1\boxtimes k}$

para todos ${\displaystyle k\in K.}$ Es sencillo verificar que esta definición satisface los axiomas de una coalgebra: es decir, que

${\displaystyle (\mathrm {id} _{TV}\boxtimes \Delta )\circ \Delta =(\Delta \boxtimes \mathrm {id} _{TV})\circ \Delta }$

donde ${\displaystyle \mathrm {id} _{TV}:x\mapsto x}$ es el mapa de identidad en ${\displaystyle TV}$. De hecho, uno obtiene

${\displaystyle ((\mathrm {id} _{TV}\boxtimes \Delta )\circ \Delta )(v)=v\boxtimes 1\boxtimes 1+1\boxtimes v\boxtimes 1+1\boxtimes 1\boxtimes v}$

y lo mismo para el otro lado. En este punto, uno podría invocar un lema y decir que${\displaystyle \Delta }$ se extiende trivialmente, por linealidad, a todos los ${\displaystyle TV}$, porque ${\displaystyle TV}$es un objeto libre y${\displaystyle V}$es un generador del álgebra libre, y${\displaystyle \Delta }$es un homomorfismo. Sin embargo, es útil proporcionar expresiones explícitas. Entonces, para${\displaystyle v\otimes w\in T^{2}V}$, uno tiene (por definición) el homomorfismo

${\displaystyle \Delta :v\otimes w\mapsto \Delta (v)\otimes \Delta (w)}$

Expandiéndose, uno tiene

${\displaystyle {\begin{aligned}\Delta (v\otimes w)&=(v\boxtimes 1+1\boxtimes v)\otimes (w\boxtimes 1+1\boxtimes w)\\&=(v\otimes w)\boxtimes 1+v\boxtimes w+w\boxtimes v+1\boxtimes (v\otimes w)\end{aligned}}}$

En la expansión anterior, no es necesario escribir ${\displaystyle 1\otimes v}$ya que esto es una simple multiplicación escalar en el álgebra; es decir, uno tiene trivialmente que${\displaystyle 1\otimes v=1\cdot v=v.}$

La extensión anterior conserva la calificación de álgebra. Eso es,

${\displaystyle \Delta :T^{2}V\to \bigoplus _{k=0}^{2}T^{k}V\boxtimes T^{(2-k)}V}$

Continuando de esta manera, se puede obtener una expresión explícita para el coproducto que actúa sobre un elemento homogéneo de orden m :

${\displaystyle {\begin{aligned}\Delta (v_{1}\otimes \cdots \otimes v_{m})&=\Delta (v_{1})\otimes \cdots \otimes \Delta (v_{m})\\&=\sum _{p=0}^{m}\left(v_{0}\otimes \cdots \otimes v_{p}\right)\;\omega \;\left(v_{p+1}\otimes \cdots \otimes v_{m}\right)\\&=\sum _{p=0}^{m}\;\sum _{\sigma \in \mathrm {Sh} (p,m-p+1)}\;\left(v_{\sigma (0)}\otimes \dots \otimes v_{\sigma (p)}\right)\boxtimes \left(v_{\sigma (p+1)}\otimes \dots \otimes v_{\sigma (m)}\right)\end{aligned}}}$

donde el ${\displaystyle \omega }$El símbolo, que debería aparecer como ø, el sha, denota el producto aleatorio . Esto se expresa en la segunda suma, que se toma sobre todos los (p, m-p + 1) -shuffles . Lo anterior está escrito con un truco de notación, para realizar un seguimiento del elemento de campo 1: el truco es escribir${\displaystyle v_{0}=1}$, y esto se baraja en varias ubicaciones durante la expansión de la suma sobre barajas. La mezcla se sigue directamente del primer axioma de una coálgebra: el orden relativo de los elementos.${\displaystyle v_{k}}$se conserva en el riffle shuffle: el riffle shuffle simplemente divide la secuencia ordenada en dos secuencias ordenadas, una a la izquierda y otra a la derecha. Cualquiera que se le dé barajar obedece

${\displaystyle \sigma (0)<\cdots <\sigma (p)\quad {\mbox{ and }}\quad \sigma (p+1)<\cdots <\sigma (m)}$

Como antes, la calificación de álgebra se conserva:

${\displaystyle \Delta :T^{m}V\to \bigoplus _{k=0}^{m}T^{k}V\boxtimes T^{(m-k)}V}$

Cuenta

El recuento ${\displaystyle \epsilon :TV\to K}$viene dada por la proyección del componente de campo a partir del álgebra. Esto se puede escribir como${\displaystyle \epsilon :v\mapsto 0}$ por ${\displaystyle v\in V}$ y ${\displaystyle \epsilon :k\mapsto k}$ por ${\displaystyle k\in K=T^{0}V}$. Por homomorfismo bajo el producto tensorial${\displaystyle \otimes }$, esto se extiende a

${\displaystyle \epsilon :x\mapsto 0}$

para todos ${\displaystyle x\in T^{1}V\oplus T^{2}V\oplus \cdots }$Es un asunto sencillo verificar que este recuento satisface el axioma necesario para la coalgebra:

${\displaystyle (\mathrm {id} \boxtimes \epsilon )\circ \Delta =\mathrm {id} =(\epsilon \boxtimes \mathrm {id} )\circ \Delta .}$

Trabajando esto explícitamente, uno tiene

${\displaystyle {\begin{aligned}((\mathrm {id} \boxtimes \epsilon )\circ \Delta )(x)&=(\mathrm {id} \boxtimes \epsilon )(1\boxtimes x+x\boxtimes 1)\\&=1\boxtimes \epsilon (x)+x\boxtimes \epsilon (1)\\&=0+x\boxtimes 1\\&\cong x\end{aligned}}}$

donde, para el último paso, se ha hecho uso del isomorfismo ${\displaystyle TV\boxtimes K\cong TV}$, como es apropiado para el axioma definitorio del recuento.

Bialgebra

Una bialgebra define tanto la multiplicación como la comultiplicación, y requiere que sean compatibles.

Multiplicación

La multiplicación viene dada por un operador

${\displaystyle \nabla :TV\boxtimes TV\to TV}$

que, en este caso, ya se dio como el producto tensorial "interno". Eso es,

${\displaystyle \nabla :x\boxtimes y\mapsto x\otimes y}$

Eso es, ${\displaystyle \nabla (x\boxtimes y)=x\otimes y.}$ Lo anterior debe dejar en claro por qué el ${\displaystyle \boxtimes }$ es necesario utilizar el símbolo: el ${\displaystyle \otimes }$ en realidad era lo mismo que ${\displaystyle \nabla }$; y el descuido de la notación aquí conduciría al caos total. Para fortalecer esto: el producto tensorial${\displaystyle \otimes }$ del álgebra tensorial corresponde a la multiplicación ${\displaystyle \nabla }$ utilizado en la definición de un álgebra, mientras que el producto tensorial ${\displaystyle \boxtimes }$es el requerido en la definición de comultiplicación en una coalgebra. ¡Estos dos productos tensoriales no son lo mismo!

Unidad

La unidad para el álgebra

${\displaystyle \eta :K\to TV}$

es solo la incrustación, de modo que

${\displaystyle \eta :k\mapsto k}$

Que la unidad es compatible con el producto tensor. ${\displaystyle \otimes }$es "trivial": es solo parte de la definición estándar del producto tensorial de espacios vectoriales. Eso es,${\displaystyle k\otimes x=kx}$para el elemento de campo ky cualquier${\displaystyle x\in TV.}$ De manera más detallada, los axiomas para un álgebra asociativa requieren los dos homomorfismos (o diagramas de conmutación):

${\displaystyle \nabla \circ (\eta \boxtimes \mathrm {id} _{TV})=\eta \otimes \mathrm {id} _{TV}=\eta \cdot \mathrm {id} _{TV}}$

en ${\displaystyle K\boxtimes TV}$, y que simétricamente, en ${\displaystyle TV\boxtimes K}$, ese

${\displaystyle \nabla \circ (\mathrm {id} _{TV}\boxtimes \eta )=\mathrm {id} _{TV}\otimes \eta =\mathrm {id} _{TV}\cdot \eta }$

donde el lado derecho de estas ecuaciones debe entenderse como el producto escalar.

Compatibilidad

La unidad y el recuento, y la multiplicación y la comultiplicación, deben satisfacer las condiciones de compatibilidad. Es sencillo ver que

${\displaystyle \epsilon \circ \eta =\mathrm {id} _{K}.}$

Del mismo modo, la unidad es compatible con la multiplicación:

${\displaystyle \Delta \circ \eta =\eta \boxtimes \eta \cong \eta }$

Lo anterior requiere el uso del isomorfismo ${\displaystyle K\boxtimes K\cong K}$para que funcione; sin esto, se pierde linealidad. En cuanto a componentes,

${\displaystyle (\Delta \circ \eta )(k)=\Delta (k)=k(1\boxtimes 1)\cong k}$

con el lado derecho haciendo uso del isomorfismo.

La multiplicación y la cuenta son compatibles:

${\displaystyle (\epsilon \circ \nabla )(x\boxtimes y)=\epsilon (x\otimes y)=0}$

siempre que x o y no son elementos de${\displaystyle K}$, y de lo contrario, uno tiene multiplicación escalar en el campo: ${\displaystyle k_{1}\otimes k_{2}=k_{1}k_{2}.}$ El más difícil de verificar es la compatibilidad de multiplicación y comultiplicación:

${\displaystyle \Delta \circ \nabla =(\nabla \boxtimes \nabla )\circ (\mathrm {id} \boxtimes \tau \boxtimes \mathrm {id} )\circ (\Delta \boxtimes \Delta )}$

donde ${\displaystyle \tau (x\boxtimes y)=y\boxtimes x}$intercambia elementos. La condición de compatibilidad solo debe verificarse en${\displaystyle V\subset TV}$; la compatibilidad total sigue como una extensión homomórfica a todos los${\displaystyle TV.}$La verificación es detallada pero sencilla; no se da aquí, excepto por el resultado final:

${\displaystyle (\Delta \circ \nabla )(v\boxtimes w)=\Delta (v\otimes w)}$

Para ${\displaystyle v,w\in V,}$ una expresión explícita para esto se dio en la sección de coalgebra, arriba.

Álgebra de Hopf

El álgebra de Hopf agrega una antípoda a los axiomas de bialgebra. La antípoda${\displaystyle S}$ en ${\displaystyle k\in K=T^{0}V}$ es dado por

${\displaystyle S(k)=k}$

A esto a veces se le llama "anti-identidad". La antípoda en${\displaystyle v\in V=T^{1}V}$ es dado por

${\displaystyle S(v)=-v}$

y en ${\displaystyle v\otimes w\in T^{2}V}$ por

${\displaystyle S(v\otimes w)=S(w)\otimes S(v)=w\otimes v}$

Esto se extiende homomórficamente a

${\displaystyle {\begin{aligned}S(v_{1}\otimes \cdots \otimes v_{m})&=S(v_{m})\otimes \cdots \otimes S(v_{1})\\&=(-1)^{m}v_{m}\otimes \cdots \otimes v_{1}\end{aligned}}}$

Compatibilidad

La compatibilidad de la antípoda con la multiplicación y la comultiplicación requiere que

${\displaystyle \nabla \circ (S\boxtimes \mathrm {id} )\circ \Delta =\eta \circ \epsilon =\nabla \circ (\mathrm {id} \boxtimes S)\circ \Delta }$

Esto es sencillo de verificar por componentes en ${\displaystyle k\in K}$:

${\displaystyle {\begin{aligned}(\nabla \circ (S\boxtimes \mathrm {id} )\circ \Delta )(k)&=(\nabla \circ (S\boxtimes \mathrm {id} ))(1\boxtimes k)\\&=\nabla (1\boxtimes k)\\&=1\otimes k\\&=k\end{aligned}}}$

Del mismo modo, en ${\displaystyle v\in V}$:

${\displaystyle {\begin{aligned}(\nabla \circ (S\boxtimes \mathrm {id} )\circ \Delta )(v)&=(\nabla \circ (S\boxtimes \mathrm {id} ))(v\boxtimes 1+1\boxtimes v)\\&=\nabla (-v\boxtimes 1+1\boxtimes v)\\&=-v\otimes 1+1\otimes v\\&=-v+v\\&=0\end{aligned}}}$

Recordar que

${\displaystyle (\eta \circ \epsilon )(k)=\eta (k)=k}$

y eso

${\displaystyle (\eta \circ \epsilon )(x)=\eta (0)=0}$

para cualquier ${\displaystyle x\in TV}$eso no esta en${\displaystyle K.}$

Se puede proceder de manera similar, por homomorfismo, verificando que la antípoda inserta los signos cancelativos apropiados en el shuffle, comenzando con la condición de compatibilidad en ${\displaystyle T^{2}V}$ y procediendo por inducción.

Cofree cocompleta coalgebra

Se puede definir un coproducto diferente en el álgebra tensorial, más simple que el dado anteriormente. Es dado por

${\displaystyle \Delta (v_{1}\otimes \dots \otimes v_{k}):=\sum _{j=0}^{k}(v_{0}\otimes \dots \otimes v_{j})\boxtimes (v_{j+1}\otimes \dots \otimes v_{k+1})}$

Aquí, como antes, se usa el truco de la notación ${\displaystyle v_{0}=v_{k+1}=1\in K}$ (recordando que ${\displaystyle v\otimes 1=v}$ trivialmente).

Este coproducto da lugar a una coalgebra. Se describe un coalgebra que es dual a la estructura de álgebra en T ( V ^* ), donde V ^* denota el espacio vectorial dual de lineal mapea V → F . De la misma manera que el álgebra tensorial es un álgebra libre , la coalgebra correspondiente se denomina co-libre co-completa. Con el producto habitual esto no es una bialgebra. Se puede convertir en bialgebra con el producto.${\displaystyle v_{i}\cdot v_{j}=(i,j)v_{i+j}}$donde (i, j) denota el coeficiente binomial para${\displaystyle {\tbinom {i+j}{i}}}$. Esta bialgebra se conoce como el álgebra de Hopf de potencia dividida .

La diferencia entre este y el otro coalgebra se ve más fácilmente en el ${\displaystyle T^{2}V}$término. Aquí uno tiene eso

${\displaystyle \Delta (v\otimes w)=1\boxtimes (v\otimes w)+v\boxtimes w+(v\otimes w)\boxtimes 1}$

por ${\displaystyle v,w\in V}$, al que claramente le falta un término mezclado, en comparación con antes.

Ver también

• Espacio vectorial trenzado
• Álgebra de Hopf trenzada
• Categoría monoidal
• Álgebra multilineal
• Álgebra de amor y tensor de Stanisław Lem
• Espacio fock

Referencias

• Bourbaki, Nicolas (1989). Álgebra I. Capítulos 1-3 . Elementos de las matemáticas. Springer-Verlag . ISBN 3-540-64243-9. (Ver Capítulo 3 §5)

• Serge Lang (2002), Álgebra , Textos de posgrado en matemáticas , 211 (3.a ed.), Springer Verlag , ISBN 978-0-387-95385-4