En geometría , un politopo (un polígono , poliedro o mosaico, por ejemplo) es isogonal o transitivo de vértice si todos sus vértices son equivalentes bajo las simetrías de la figura. Esto implica que cada vértice está rodeado por los mismos tipos de caras en el mismo orden o en orden inverso, y con los mismos ángulos entre las caras correspondientes.
Técnicamente, decimos que para dos vértices cualesquiera existe una simetría del politopo que asigna el primero isométricamente al segundo. Otras formas de decir esto son que el grupo de automorfismos del politopo actúa transitivamente sobre sus vértices, o que los vértices se encuentran dentro de una sola órbita de simetría .
Todos los vértices de una figura isogonal n- dimensional finita existen en una ( n −1) -esfera . [ cita requerida ]
El término isogonal se ha utilizado durante mucho tiempo para los poliedros. Vértice-transitivo es un sinónimo tomado de ideas modernas como los grupos de simetría y la teoría de grafos .
El pseudorhombicuboctaedro - que no es isogonal - demuestra que simplemente afirmar que "todos los vértices se ven iguales" no es tan restrictivo como la definición utilizada aquí, que involucra al grupo de isometrías preservando el poliedro o mosaico.
Polígonos isogonales y apeirogones
| isogonales- apeirogons |
|---|
 |
| Apeirogons de sesgo isogonal |
Todos los polígonos regulares , apeirogones y polígonos de estrellas regulares son isogonales . El dual de un polígono isogonal es un polígono isotoxal .
Algunos polígonos de lados pares y apeirogones que alternan dos longitudes de borde, por ejemplo, un rectángulo , son isogonales .
Todos los gones 2 n isogonales planos tienen simetría diedro (D n , n = 2, 3, ...) con líneas de reflexión a través de los puntos del borde medio.
| D 2 | D 3 | D 4 | D 7 |
|---|---|---|---|
 Rectángulos isogonales y rectángulos cruzados que comparten la misma disposición de vértices | 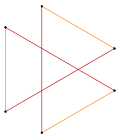 Hexagrama isogonal con 6 vértices idénticos y 2 longitudes de arista. [1] | 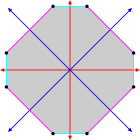 Isogonal convexa octógono con líneas radiales azules y rojas de reflexión | 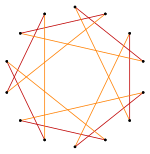 Isogonal "estrella" tetradecágono con un tipo vértice, y dos tipos de borde [2] |
Poliedros isogonales y mosaicos 2D
 |
| Azulejos cuadrados distorsionados |
 |
| Un mosaico cuadrado truncado distorsionado |
Un poliedro isogonal y un mosaico 2D tienen un solo tipo de vértice. Un poliedro isogonal con todas las caras regulares también es un poliedro uniforme y se puede representar mediante una notación de configuración de vértice que secuencia las caras alrededor de cada vértice. Las variaciones geométricamente distorsionadas de poliedros uniformes y teselaciones también pueden recibir la configuración de vértice.
| D 3d , orden 12 | T h , orden 24 | O h , orden 48 | |
|---|---|---|---|
| 4.4.6 | 3.4.4.4 | 4.6.8 | 3.8.8 |
 Un prisma hexagonal distorsionado (trapezoprisma ditrigonal) |  Un rombicuboctaedro distorsionado | 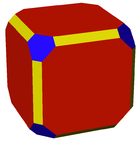 Un cuboctaedro truncado poco profundo |  Un cubo hipertruncado |
Los poliedros isogonales y los mosaicos 2D pueden clasificarse además:
- Regular si también es isoédrico (transitivo por caras) e isotoxal (transitivo por bordes); esto implica que cada cara es el mismo tipo de polígono regular .
- Cuasi regular si también es isotoxal (transitivo por los bordes) pero no isoédrico (transitivo por las caras).
- Semi-regular si cada cara es un polígono regular pero no es isoédrico (transitivo por caras) o isotoxal (transitivo por aristas). (La definición varía entre los autores; por ejemplo, algunos excluyen sólidos con simetría diedro o sólidos no convexos).
- Uniforme si cada cara es un polígono regular, es decir, es regular, cuasirregular o semi-regular.
- Semi-uniforme si sus elementos también son isogonales.
- Escaliforme si todos los bordes tienen la misma longitud.
- Noble si también es isoédrico (cara transitiva).
N dimensiones: politopos y teselados isogonales
Estas definiciones se pueden extender a politopos y teselaciones de dimensiones superiores . Todos los politopos uniformes son isogonales , por ejemplo, los 4 politopos uniformes y los panales uniformes convexos .
El dual de un politopo isogonal es una figura isoédrica , que es transitiva en sus facetas .
k - figuras isogonales y k- uniformes
Un politopo o mosaico puede llamarse k -isogonal si sus vértices forman k clases de transitividad. Un término más restrictivo, k -uniforme se define como una figura k-isogonal construida solo a partir de polígonos regulares . Se pueden representar visualmente con colores mediante diferentes coloraciones uniformes .
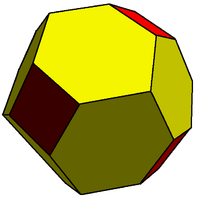 Este dodecaedro rómbico truncado es 2-isogonal porque contiene dos clases de transitividad de vértices. Este poliedro está formado por cuadrados y hexágonos aplanados . |  Este mosaico semirregular también es 2-isogonal (y 2-uniforme ). Este mosaico está formado por un triángulo equilátero y caras hexagonales regulares . |  Eneagrama 2-isogonal 9/4 (cara de la estelación final del icosaedro ) |
Ver también
- Edge-transititive (figura isotoxal)
- Cara transitiva (figura isoédrica)
Referencias
- ^ Coxeter, Las densidades de los politopos regulares II, p54-55, figura del vértice del "hexagrama" de h {5 / 2,5}.
- ^ El lado más ligero de las matemáticas: Actas de la Conferencia conmemorativa de Eugène Strens sobre matemáticas recreativas y su historia , (1994), Metamorfosis de polígonos , Branko Grünbaum , Figura 1. Parámetro t = 2.0
- Peter R. Cromwell, Polyhedra , Cambridge University Press 1997, ISBN 0-521-55432-2 , pág. 369 Transitividad
- Grünbaum, Branko ; Shephard, GC (1987). Azulejos y Patrones . WH Freeman and Company. ISBN 0-7167-1193-1.(p. 33 k- mosaicos isogonales , p. 65 k-mosaicos uniformes )
Enlaces externos
- Weisstein, Eric W. "Gráfico transitivo de vértice" . MathWorld .
- Olshevsky, George. "Transitividad" . Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
- Olshevsky, George. "Isogonal" . Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
- Poliedros caleidoscópicos isogonales Vladimir L. Bulatov , Departamento de Física, Universidad Estatal de Oregón, Corvallis, Presentado en Mosaic2000, Simposio abierto milenario sobre las artes y la informática interdisciplinaria, 21-24 de agosto de 2000, Seattle, WA Modelos VRML
- Steven Dutch usa el término k-uniforme para enumerar teselaciones k-isogonales
- Lista de mosaicos n-uniformes
- Weisstein, Eric W. "Teselaciones demirregulares" . MathWorld . (También usa el término k-uniform para k-isogonal)