Límite (teoría de categorías)

En la teoría de categorías , una rama de las matemáticas , la noción abstracta de límite captura las propiedades esenciales de construcciones universales como productos , retrocesos y límites inversos . La noción dual de colimit generaliza construcciones como uniones disjuntas , sumas directas , coproductos , expulsiones y límites directos .

Los límites y colimits, como las nociones fuertemente relacionadas de propiedades universales y functores adjuntos , existen en un alto nivel de abstracción. Para comprenderlos, es útil estudiar primero los ejemplos específicos que estos conceptos pretenden generalizar.

Definición

Límites y colimits en una categoría ${\ Displaystyle C}$ se definen mediante diagramas en ${\ Displaystyle C}$ . Formalmente, un diagrama de forma ${\ Displaystyle J}$ en ${\ Displaystyle C}$ es un functor de ${\ Displaystyle J}$ para ${\ Displaystyle C}$ :

{\ Displaystyle F: J \ a C.}

La categoría ${\ Displaystyle J}$ se considera una categoría de índice , y el diagrama ${\ Displaystyle F}$ se piensa que indexa una colección de objetos y morfismos en ${\ Displaystyle C}$ estampado en ${\ Displaystyle J}$ .

Uno está más a menudo interesado en el caso donde la categoría ${\ Displaystyle J}$ es una categoría pequeña o incluso finita . Se dice que un diagrama es pequeño o finito siempre que ${\ Displaystyle J}$ es.

Límites

Dejar ${\ Displaystyle F: J \ to C}$ ser un diagrama de forma ${\ Displaystyle J}$ en una categoría ${\ Displaystyle C}$ . Un cono para ${\ Displaystyle F}$ es un objeto ${\ Displaystyle N}$ de ${\ Displaystyle C}$ junto con una familia ${\ Displaystyle \ psi _ {X}: N \ a F (X)}$ de morfismos indexados por los objetos ${\ Displaystyle X}$ de ${\ Displaystyle J}$ , tal que por cada morfismo ${\ Displaystyle f: X \ to Y}$ en ${\ Displaystyle J}$ , tenemos ${\ Displaystyle F (f) \ circ \ psi _ {X} = \ psi _ {Y}}$ .

Un límite del diagrama ${\ Displaystyle F: J \ to C}$ es un cono ${\ Displaystyle (L, \ phi)}$ para ${\ Displaystyle F}$ tal que por cada otro cono ${\ Displaystyle (N, \ psi)}$ para ${\ Displaystyle F}$ existe un morfismo único ${\ Displaystyle u: N \ a L}$ tal que ${\ Displaystyle \ phi _ {X} \ circ u = \ psi _ {X}}$ para todos ${\ Displaystyle X}$ en ${\ Displaystyle J}$ .

Uno dice que el cono ${\ Displaystyle (N, \ psi)}$ factores a través del cono ${\ Displaystyle (L, \ phi)}$ con la factorización única ${\ Displaystyle u}$ . El morfismo ${\ Displaystyle u}$ a veces se le llama morfismo mediador .

Los límites también se conocen como conos universales , ya que se caracterizan por una propiedad universal (consulte a continuación para obtener más información). Al igual que con toda propiedad universal, la definición anterior describe un estado equilibrado de generalidad: el objeto límite ${\ Displaystyle L}$ tiene que ser lo suficientemente general para permitir que cualquier otro cono lo atraviese; en la otra mano, ${\ Displaystyle L}$ tiene que ser lo suficientemente específico, de modo que solo sea posible una factorización de este tipo para cada cono.

Los límites también se pueden caracterizar como objetos terminales en la categoría de los conos a F .

Es posible que un diagrama no tenga ningún límite. Sin embargo, si un diagrama tiene un límite, este límite es esencialmente único: es único hasta un isomorfismo único . Por esta razón, a menudo se habla de la límite de F .

Colimits

Las nociones duales de límites y conos son colimits y co-conos. Aunque es sencillo obtener las definiciones de estos invirtiendo todos los morfismos en las definiciones anteriores, los declararemos explícitamente aquí:

Un co-cono de un diagrama ${\ Displaystyle F: J \ to C}$ es un objeto ${\ Displaystyle N}$ de ${\ Displaystyle C}$ junto con una familia de morfismos

{\ Displaystyle \ psi _ {X}: F (X) \ a N}

para cada objeto ${\ Displaystyle X}$ de ${\ Displaystyle J}$ , tal que por cada morfismo ${\ Displaystyle f: X \ to Y}$ en ${\ Displaystyle J}$ , tenemos ${\ Displaystyle \ psi _ {Y} \ circ F (f) = \ psi _ {X}}$ .

Un colimit de un diagrama ${\ Displaystyle F: J \ to C}$ es un co-cono ${\ Displaystyle (L, \ phi)}$ de ${\ Displaystyle F}$ tal que para cualquier otro co-cono ${\ Displaystyle (N, \ psi)}$ de ${\ Displaystyle F}$ existe un morfismo único ${\ Displaystyle u: L \ a N}$ tal que ${\ Displaystyle u \ circ \ phi _ {X} = \ psi _ {X}}$ para todos ${\ Displaystyle X}$ en ${\ Displaystyle J}$ .

Los colimits también se conocen como co-conos universales . Se pueden caracterizar como objetos iniciales en la categoría de co-conos de ${\ Displaystyle F}$ .

Al igual que con los límites, si un diagrama ${\ Displaystyle F}$ tiene un colimit, entonces este colimit es único hasta un isomorfismo único.

Variaciones

También se pueden definir límites y colimits para colecciones de objetos y morfismos sin el uso de diagramas. Las definiciones son las mismas (tenga en cuenta que en las definiciones anteriores nunca necesitamos usar la composición de morfismos en ${\ Displaystyle J}$ ). Esta variación, sin embargo, no agrega información nueva. Cualquier colección de objetos y morfismos define un grafo dirigido (posiblemente grande) ${\ Displaystyle G}$ . Si dejamos ${\ Displaystyle J}$ ser la categoría gratuita generada por ${\ Displaystyle G}$ , hay un diagrama universal ${\ Displaystyle F: J \ to C}$ cuya imagen contiene ${\ Displaystyle G}$ . El límite (o colimit) de este diagrama es el mismo que el límite (o colimit) de la colección original de objetos y morfismos.

El límite débil y los colimits débiles se definen como límites y colimits, excepto que se elimina la propiedad de unicidad del morfismo mediador.

Ejemplos

Límites

La definición de límites es lo suficientemente general como para incluir varias construcciones útiles en entornos prácticos. En el siguiente vamos a considerar el límite ( L , φ ) de un diagrama de F : J → C .

Objetos terminales . Si J es la categoría vacía, solo hay un diagrama de la forma J : el vacío (similar a la función vacía en la teoría de conjuntos). Un cono con el diagrama de vacío es esencialmente sólo un objeto de C . El límite de F es cualquier objeto que sea factorizado de forma única por todos los demás objetos. Esta es solo la definición de un objeto terminal .
Productos . Si J es una categoría discreta a continuación un diagrama de F es esencialmente nada más que una familia de objetos de C , indexada por J . El límite L de F se llama producto de estos objetos. El cono φ consta de una familia de morfismos φ _X : L → F ( X ) llamados proyecciones del producto. En la categoría de conjuntos , por ejemplo, los productos están dados por productos cartesianos y las proyecciones son solo proyecciones naturales sobre los diversos factores.
- Poderes . Un caso especial de un producto es cuando el diagrama F es un functor constante a un objeto X de C . El límite de este diagrama se denomina J ^º potencia de X y denotado X ^J .
Ecualizadores . Si J es una categoría con dos objetos y dos morfismos paralelas de un objeto a otro, a continuación un diagrama de la forma J es un par de morfismos paralelas en C . El límite L de tal diagrama se llama ecualizador de esos morfismos.
- Granos . Un kernel es un caso especial de un ecualizador donde uno de los morfismos es un morfismo cero .
Retrocesos . Deje que F sea un diagrama que escoge tres objetos X , Y , y Z en C , donde los morfismos único no-identidad son f : X → Z y g : Y → Z . El límite L de F se llama retroceso o producto de fibra . Se puede visualizar muy bien como un cuadrado conmutativo :

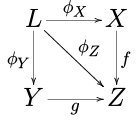
Límites inversos . Sea J un conjunto dirigido (considerado como una categoría pequeña agregando flechas i → j si y solo si i ≥ j ) y sea F : J ^op → C un diagrama. El límite de F se llama (confusamente) un límite inverso o límite proyectivo .
Si J = 1 , la categoría con un único objeto y morfismo, a continuación, un diagrama de la forma J es esencialmente sólo un objeto X de C . Un cono a un objeto X es sólo un morfismo con codomain X . Un morfismo f : Y → X es un límite del diagrama X si y solo si f es un isomorfismo . De manera más general, si J es cualquier categoría con un objeto inicial i , entonces cualquier diagrama de forma J tiene un límite, es decir, cualquier objeto isomorfo a F( i ). Tal un isomorfismo determina de forma única un cono universal a F .
Límites topológicos . Los límites de funciones son un caso especial de límites de filtros , que se relacionan con los límites categóricos de la siguiente manera. Dado un espacio topológico X , denote por F el conjunto de filtros en X , x ∈ X un punto, V ( x ) ∈ F el filtro de vecindad de x , A ∈ F un filtro particular y ${\ Displaystyle F_ {x, A} = \ {G \ in F \ mid V (x) \ cup A \ subset G \}}$ el conjunto de filtros más fino que A y que convergen ax . Los filtros F se les da una estructura de categorías pequeñas y delgadas mediante la adición de una flecha A → B si y sólo si A ⊆ B . La inyección ${\ Displaystyle I_ {x, A}: F_ {x, A} \ to F}$ se convierte en un funtor y se cumple la siguiente equivalencia:

x es un límite topológico de A si y solo si A es un límite categórico de

{\ Displaystyle I_ {x, A}}

Colimits

Los ejemplos de colimits se dan en las versiones duales de los ejemplos anteriores:

Los objetos iniciales son colimites de diagramas vacíos.
Los coproductos son colímites de diagramas indexados por categorías discretas.
- Los copowers son colimites de diagramas constantes de categorías discretas.
Los coequalizadores son colímites de un par paralelo de morfismos.
- Las coquelas son coequalizadores de un morfismo y un morfismo cero paralelo.
Los pushouts son colimites de un par de morfismos con dominio común.
Los límites directos son colímites de diagramas indexados por conjuntos dirigidos.

Propiedades

Existencia de límites

Un diagrama dado F : J → C puede o no puede tener un límite (o colimit) en C . De hecho, puede que ni siquiera haya un cono para F , y mucho menos un cono universal.

Una categoría C se dice que tienen límites de forma J si cada diagrama de la forma J tiene un límite en C . Específicamente, se dice que una categoría C

tener productos si tiene límites de forma J para cada pequeña categoría discreta J (no necesita tener productos grandes),
tener ecualizadores si tiene límites de forma ${\ Displaystyle \ bullet \ rightrightarrows \ bullet}$ (es decir, cada par paralelo de morfismos tiene un ecualizador),
tiene retrocesos si tiene límites de forma ${\ Displaystyle \ bullet \ rightarrow \ bullet \ leftarrow \ bullet}$ (es decir, cada par de morfismos con codominio común tiene un retroceso).

Una categoría completa es una categoría que tiene todos los límites pequeños (es decir, todos los límites de la forma J para cada categoría J pequeña ).

También se pueden hacer definiciones duales. Una categoría tiene colímites de forma J si cada diagrama de la forma J tiene una colimit en C . Una categoría cocompleta es aquella que tiene todos los colímites pequeños.

El teorema de existencia para los límites de los estados que si una categoría C tiene ecualizadores y todos los productos indexadas por las clases Ob ( J ) y Hom ( J ), entonces C tiene todos los límites de la forma J . En este caso, el límite de un diagrama F : J → C se puede construir como el ecualizador de los dos morfismos

{\ Displaystyle s, t: \ prod _ {i \ in \ operatorname {Ob} (J)} F (i) \ rightrightarrows \ prod _ {f \ in \ operatorname {Hom} (J)} F (\ operatorname { bacalao} (f))}

dado (en forma de componente) por

{\ Displaystyle {\ begin {alineado} s & = {\ bigl (} F (f) \ circ \ pi _ {\ operatorname {dom} (f)} {\ bigr)} _ {f \ in \ operatorname {Hom} (J)} \\ t & = {\ bigl (} \ pi _ {\ operatorname {cod} (f)} {\ bigr)} _ {f \ in \ operatorname {Hom} (J)}. \ End {alineado }}}

Existe un teorema de existencia dual para colimits en términos de coequalizadores y coproductos. Ambos de estos teoremas dan suficientes y necesarias condiciones para la existencia de los (co) límites de la forma J .

Propiedad universal

Los límites y colimits son casos especiales importantes de construcciones universales .

Sea C una categoría y sea J una pequeña categoría de índice. La categoría funtor C ^J puede ser pensado como la categoría de todos los diagramas de forma de J en C . El functor diagonal

{\ Displaystyle \ Delta: {\ mathcal {C}} \ to {\ mathcal {C}} ^ {\ mathcal {J}}}

es el funtor que asigna cada objeto N en C a la constante funtor Δ ( N ): J → C a N . Es decir, Δ ( N ) ( X ) = N para cada objeto X en J y Δ ( N ) ( f ) = id _N para cada morfismo f en J .

Dado un diagrama F : J → C (pensado como un objeto en C ^J ), una transformación natural ψ : Δ ( N ) → F (que es solo un morfismo en la categoría C ^J ) es lo mismo que un cono de N a F . Para ver esto, primero tenga en cuenta que Δ ( N ) ( X ) = N para todo X implica que los componentes de ψ son morfismos ψ _X : N → F ( X ), que todos comparten el dominioN . Además, el requisito de que los diagramas del cono se conmuten es cierto simplemente porque ψ es una transformación natural. (Doblemente, una transformación natural ψ : F → Δ ( N ) es lo mismo que un co-cono de F a N ).

Por lo tanto, las definiciones de límites y colimits pueden luego reformularse en la forma:

Un límite de F es un morfismo universal a partir de Δ a F .
Un colimit de F es un morfismo universal de F a Δ.

Adjunciones

Como todas las construcciones universales, la formación de límites y colimits es de naturaleza funcional. En otras palabras, si cada diagrama de la forma J tiene un límite en C (para J pequeño) existe un functor límite

{\ Displaystyle \ lim: {\ mathcal {C}} ^ {\ mathcal {J}} \ to {\ mathcal {C}}}

que asigna a cada diagrama su límite ya cada transformación natural η: F → G el morfismo único lim η: lim F → lim G conmutando con los conos universales correspondientes. Este funtor es adjunto derecho a la diagonal Δ funtor: C → C ^J . Esta adjunción da una biyección entre el conjunto de todos los morfismos de N a lim F y el conjunto de todos los conos de N a F

{\ Displaystyle \ operatorname {Hom} (N, \ lim F) \ cong \ operatorname {Cono} (N, F)}

que es natural en las variables N y F . El counit de esta adjunción es simplemente el cono universal a partir de lim F a F . Si la categoría de índice J está conectada (y no está vacía), entonces la unidad de la adjunción es un isomorfismo, de modo que lim es un inverso a la izquierda de Δ. Esto falla si J no está conectado. Por ejemplo, si J es una categoría discreta, los componentes de la unidad son los morfismos diagonales delta: N → N ^J .

Doblemente, si cada diagrama de la forma J tiene un colimit en C (para J pequeño) existe un functor colimit

{\ Displaystyle \ operatorname {colim}: {\ mathcal {C}} ^ {\ mathcal {J}} \ to {\ mathcal {C}}}

que asigna a cada diagrama su colimit. Este funtor se deja adjunto al funtor diagonal Δ: C → C ^J , y uno tiene un isomorfismo natural

{\ Displaystyle \ operatorname {Hom} (\ operatorname {colim} F, N) \ cong \ operatorname {Cocone} (F, N).}

La unidad de este adjunción es el cocone universal a partir de F a Colim F . Si J está conectado (y no está vacío), entonces el recuento es un isomorfismo, por lo que colim es un inverso a la izquierda de Δ.

Tenga en cuenta que tanto el functor límite como el colimit son functores covariantes .

Como representaciones de functores

Se pueden usar functores Hom para relacionar límites y colimits en una categoría C con límites en Set , la categoría de conjuntos . Esto se deduce, en parte, del hecho de la covariante Hom funtor Hom ( N , -): C → Set conserva todos los límites en C . Por dualidad, el functor Hom contravariante debe llevar colimits al límite.

Si un diagrama F : J → C tiene un límite en C , denotado por lim F , hay un isomorfismo canónico

{\ Displaystyle \ operatorname {Hom} (N, \ lim F) \ cong \ lim \ operatorname {Hom} (N, F-)}

que es natural en la variable N . Aquí el funtor Hom ( N , F -) es la composición de la Hom funtor Hom ( N , -) con F . Este isomorfismo es el único que respeta los conos limitantes.

Uno puede usar la relación anterior para definir el límite de F en C . El primer paso es observar que el límite del funtor Hom ( N , F -) se puede identificar con el conjunto de todos los conos de N a F :

{\ displaystyle \ lim \ operatorname {Hom} (N, F -) = \ operatorname {Cone} (N, F).}

El cono de limitación está dada por la familia de mapas pi _X : Cono ( N , F ) → Hom ( N , FX ) donde $π$ _X ( ψ ) = ψ _X . Si se le da un objeto L de C junto con un isomorfismo natural Φ : Hom (-, L ) → Cono (-, F ), el objeto L será un límite de F con el cono límite dado por Φ _L (id _L ). En lenguaje elegante, esto equivale a decir que un límite de Fes una representación del functor Cono (-, F ): C → Conjunto .

Doblemente, si un diagrama F : J → C tiene un colimit en C , denotado colim F , hay un isomorfismo canónico único

{\ Displaystyle \ operatorname {Hom} (\ operatorname {colim} F, N) \ cong \ lim \ operatorname {Hom} (F-, N)}

que es natural en la variable N y respeta los conos colimitantes. Identificando el límite de Hom ( F -, N ) con el conjunto Cocone ( F , N ), esta relación puede usarse para definir el colimit del diagrama F como una representación del funtor Cocone ( F , -).

Intercambio de límites y colimits de conjuntos

Sea I una categoría finita y J una pequeña categoría filtrada . Para cualquier bifunctor

{\ Displaystyle F: I \ times J \ to \ mathbf {Set},}

hay un isomorfismo natural

{\ Displaystyle \ operatorname {colim} \ limits _ {J} \ lim _ {I} F (i, j) \ rightarrow \ lim _ {I} \ operatorname {colim} \ limits _ {J} F (i, j ).}

En palabras, los colimits filtrados en Establecer conmutan con límites finitos. También sostiene que los límites pequeños se conmutan con los límites pequeños. ^[1]

Funciones y límites

Si F : J → C es un diagrama en C y G : C → D es un funtor entonces por la composición (recuérdese que un diagrama es sólo un funtor) se obtiene un diagrama de GF : J → D . Entonces, una pregunta natural es:

"¿Cómo se relacionan los límites de GF con los de F ?"

Preservación de límites

Un functor G : C → D induce un mapa de Cono ( F ) a Cono ( GF ): si Ψ es un cono de N a F, entonces GΨ es un cono de GN a GF . El funtor G se dice que preservar los límites de F si ( GL , Gφ ) es un límite de GF siempre que ( L , φ ) es un límite de F . (Tenga en cuenta que si el límite de F no existe, entonces G conserva al vacío los límites de F. )

Un funtor G se dice que preservar todos los límites de la forma J si conserva los límites de todos los diagramas F : J → C . Por ejemplo, se puede decir que G conserva productos, ecualizadores, retrocesos, etc. Un funtor continuo es aquel que conserva todos los límites pequeños .

Se pueden hacer definiciones análogas para colimits. Por ejemplo, un funtor G conserva los colímites de F si G ( L , φ ) es un colimit de GF siempre que ( L , φ ) es un colimit de F . Un functor cocontinuo es aquel que conserva todos los colímites pequeños .

Si C es una categoría completa , entonces, según el teorema de existencia anterior para los límites, un funtor G : C → D es continuo si y solo si conserva productos (pequeños) y ecualizadores. Dualmente, G es cocontinuo si y solo si conserva (pequeños) coproductos y coequalizadores.

Una propiedad importante de los functores adjuntos es que todo functor adjunto derecho es continuo y todo functor adjunto izquierdo es cocontinuo. Dado que los functores adjuntos existen en abundancia, esto da numerosos ejemplos de functores continuos y cocontinuos.

Para un diagrama dado F : J → C y el functor G : C → D , si tanto F como GF tienen límites especificados, existe un morfismo canónico único

{\ Displaystyle \ tau _ {F}: G \ lim F \ to \ lim GF}

que respeta los conos límite correspondientes. El funtor G conserva los límites de F si y solo este mapa es un isomorfismo. Si las categorías C y D tienen todos los límites de la forma J, entonces lim es un funtor y los morfismos τ _F forman los componentes de una transformación natural.

{\ Displaystyle \ tau: G \ lim \ to \ lim G ^ {J}.}

El funtor G conserva todos los límites de la forma J si y solo si τ es un isomorfismo natural. En este sentido, se puede decir que el funtor G conmuta con límites ( hasta un isomorfismo natural canónico).

La preservación de límites y colimits es un concepto que solo se aplica a los functores covariantes . Para los functores contravariantes, las nociones correspondientes serían un funtor que lleva colimits a límites, o uno que lleva límites a colimits.

Levantamiento de límites

Se dice que un funtor G : C → D eleva los límites de un diagrama F : J → C si siempre que ( L , φ ) es un límite de GF existe un límite ( L ′, φ ′) de F tal que G ( L ′, Φ ′) = ( L , φ ). Un funtor G eleva los límites de la forma J si eleva los límites de todos los diagramas de la forma J. Por lo tanto, se puede hablar de productos de elevación, ecualizadores, retrocesos, etc. Finalmente, se dice que G eleva los límites si supera todos los límites. Hay dos definiciones para el levantamiento de colímites.

Un funtor G eleva los límites únicamente para un diagrama F si hay un cono de preimagen único ( L ′, φ ′) tal que ( L ′, φ ′) es un límite de F y G ( L ′, φ ′) = ( L , φ ). Se puede demostrar que G eleva los límites únicamente si y solo si eleva los límites y es amnésico .

El levantamiento de los límites está claramente relacionado con la preservación de los límites. Si G ascensores límites para un diagrama de F y GF tiene un límite, entonces F también tiene un límite y G conserva los límites de F . Resulta que:

Si G eleva los límites de toda la forma J y D tiene todos los límites de la forma J , entonces C también tiene todos los límites de la forma J y G conserva estos límites.
Si G eleva todos los límites pequeños y D está completo, entonces C también está completo y G es continuo.

Las declaraciones duales para colimits son igualmente válidas.

Creación y reflejo de límites

Sea F : J → C un diagrama. Se dice que un funtor G : C → D

crear límites para F si siempre que ( L , φ ) es un límite de GF existe un cono único ( L ′, φ ′) a F tal que G ( L ′, φ ′) = ( L , φ ), y además, este cono es un límite de F .
reflejar límites para F si cada cono a F cuya imagen bajo G es un límite de GF está ya un límite de F .

Dualmente, se puede definir creación y reflejo de colimits.

Las siguientes declaraciones se ven fácilmente como equivalentes:

El functor G crea límites.
El functor G eleva los límites de forma única y refleja los límites.

Hay ejemplos de functores que elevan los límites de forma única pero que ni los crean ni los reflejan.

Ejemplos

Cada functor representable C → Set conserva límites (pero no necesariamente colimits). En particular, para cualquier objeto A de C , esto es cierto para el functor Hom covariante Hom ( A , -): C → Set .
El functor olvidadizo U : Grp → Set crea (y conserva) todos los límites pequeños y colimits filtrados ; sin embargo, U no conserva los coproductos. Esta situación es típica de los functores olvidadizos algebraicos.
El functor libre F : Conjunto → Grp (que asigna a cada conjunto S el grupo libre sobre S ) se deja adjunto al functor olvidadizo U y es, por tanto, cocontinuo. Esto explica por qué el producto libre de dos grupos libres G y H es el grupo libre generado por la unión de la desunión de los generadores de G y H .
El functor de inclusión Ab → Grp crea límites pero no preserva los coproductos (el coproducto de dos grupos abelianos es la suma directa ).
El functor olvidadizo Top → Set eleva los límites y colimits de forma única, pero no crea ninguno.
Sea Met _c la categoría de espacios métricos con funciones continuas para morfismos. El functor olvidadizo Met _c → Set eleva límites finitos pero no los eleva únicamente.

Una nota sobre terminología

La terminología más antigua se refería a los límites como "límites inversos" o "límites proyectivos" y a los colímites como "límites directos" o "límites inductivos". Esta ha sido la fuente de mucha confusión.

Hay varias formas de recordar la terminología moderna. Ante todo,

cokernels,
coproductos,
coequalizadores, y
coddominios

son tipos de colimits, mientras que

granos
productos
ecualizadores, y
dominios

son tipos de límites. En segundo lugar, el prefijo "co" implica "primera variable de la ${\ Displaystyle \ operatorname {Hom}}$ ". Términos como" cohomología "y" cofibración "tienen todos una asociación ligeramente más fuerte con la primera variable, es decir, la variable contravariante, de la ${\ Displaystyle \ operatorname {Hom}}$ bifunctor.

Ver también

Categoría cerrada cartesiana : tipo de categoría en la teoría de categorías
Ecualizador (matemáticas) : conjunto de argumentos donde dos o más funciones tienen el mismo valor
Límite inverso
Producto (teoría de categorías) : objeto generalizado en la teoría de categorías

Referencias

^ "límite" . nLab .

Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Categorías abstractas y concretas (PDF) . John Wiley e hijos. ISBN 0-471-60922-6.
Mac Lane, Saunders (1998). Categorías para el matemático que trabaja . Textos de Posgrado en Matemáticas . 5 (2ª ed.). Springer-Verlag . ISBN 0-387-98403-8. Zbl 0906.18001 .
Borceux, Francis (1994). "Límites". Manual de álgebra categórica . Enciclopedia de las matemáticas y sus aplicaciones 50-51, 53 [es decir, 52]. Volumen 1. Cambridge University Press. ISBN 0-521-44178-1. |volume=tiene texto extra ( ayuda )

Enlaces externos

Página web interactiva que genera ejemplos de límites y colimits en la categoría de conjuntos finitos. Escrito por Jocelyn Paine .
Límite en nLab

[1] "límite" . nLab .