Monodromía

La parte imaginaria del logaritmo complejo . Intentar definir el logaritmo complejo en C \ {0} da diferentes respuestas a lo largo de diferentes caminos. Esto conduce a un grupo monodromía cíclico infinito y una cubierta de C \ {0} por un helicoide (un ejemplo de una superficie de Riemann ).

En matemáticas , la monodromía es el estudio de cómo los objetos del análisis matemático , la topología algebraica , la geometría algebraica y la geometría diferencial se comportan cuando "corren alrededor" de una singularidad . Como su nombre lo indica, el significado fundamental de monodromía proviene de "correr solos". Está estrechamente asociado con los mapas de cobertura y su degeneración en ramificación ; El aspecto que da lugar a los fenómenos de monodromía es que ciertas funciones que podemos desear definir no tienen un solo valor.mientras "corremos alrededor" de un camino que rodea una singularidad. El fracaso de la monodromía se puede medir definiendo un grupo de monodromía : un grupo de transformaciones que actúan sobre los datos que codifican lo que sucede cuando "corremos" en una dimensión. La falta de monodromía a veces se denomina polidromía . ^[1]

Definición

Sea $X$ un espacio topológico basado en conexión y localmente conectado con el punto base $x$ , y sea ${\ Displaystyle p: {\ tilde {X}} \ to X}$ ser una cubierta con fibra ${\ Displaystyle F = p ^ {- 1} (x)}$ . Para un bucle $γ: [0, 1] \to X$ basado en $x$ , denota una elevación debajo del mapa de cobertura, comenzando en un punto ${\ Displaystyle {\ tilde {x}} \ in F}$ , por ${\ Displaystyle {\ tilde {\ gamma}}}$ . Finalmente, denotamos por ${\ Displaystyle {\ tilde {x}} \ cdot {\ tilde {\ gamma}}}$ el punto final ${\ Displaystyle {\ tilde {\ gamma}} (1)}$ , que generalmente es diferente de ${\ Displaystyle {\ tilde {x}}}$ . Hay teoremas que establecen que esta construcción da una bien definida acción de grupo del grupo fundamental $π 1 (X, x)$ en $F$ , y que el estabilizador de ${\ Displaystyle {\ tilde {x}}}$ es exactamente ${\ Displaystyle p _ {*} \ left (\ pi _ {1} \ left ({\ tilde {X}}, {\ tilde {x}} \ right) \ right)}$ , es decir, un elemento $[γ]$ fija un punto en $F$ si y solo si está representado por la imagen de un bucle en ${\ Displaystyle {\ tilde {X}}}$ basado en ${\ Displaystyle {\ tilde {x}}}$ . Esta acción se llama acción de monodromía y el homomorfismo correspondiente $π 1 (X, x) \to Aut (H * (F x))$ en el grupo de automorfismo en $F$ es la monodromía algebraica . La imagen de este homomorfismo es el grupo de monodromía . Hay otro mapa $π 1 (X, x) \to Diff (F x) / Is (F x)$ cuya imagen se llama grupo de monodromía topológica.

Ejemplo

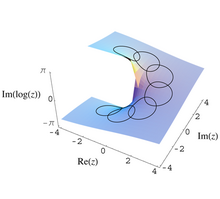
Estas ideas se explicitaron por primera vez en un análisis complejo . En el proceso de continuación analítica , una función que es una función analítica $F (z)$ en algún subconjunto abierto $E$ del plano complejo perforado $ℂ \ {0}$ puede continuar de nuevo en $E$ , pero con valores diferentes. Por ejemplo, tome

{\ Displaystyle {\ begin {alineado} F (z) & = \ log (z) \\ E & = \ {z \ in \ mathbb {C} \ mid \ operatorname {Re} (z)> 0 \} \ end {alineado}}}

luego continuación analítica en sentido antihorario alrededor del círculo

{\ Displaystyle | z | = 1}

resultará en el retorno, no a $F (z)$ sino

{\ Displaystyle F (z) +2 \ pi i}

En este caso, el grupo de monodromía es cíclico infinito y el espacio de cobertura es la cubierta universal del plano complejo perforado. Esta cobertura se puede visualizar como el helicoide (como se define en el artículo de helicoide) restringido a $ρ > 0$ . El mapa de cobertura es una proyección vertical, en cierto sentido colapsando la espiral de la manera obvia para obtener un plano pinchado.

Ecuaciones diferenciales en el dominio complejo

Una aplicación importante es la de las ecuaciones diferenciales , donde una sola solución puede dar más soluciones linealmente independientes mediante la continuación analítica . Ecuaciones diferenciales lineales definidos en un, conjunto conectado abierto S en el plano complejo tienen un grupo monodromía, que (más precisamente) es una representación lineal del grupo fundamental de S , resumiendo todos los extensión analítica bucles y vuelta en S . El problema inverso, de construir la ecuación (con singularidades regulares ), dada una representación, se llama problema de Riemann-Hilbert .

Para un sistema lineal regular (y en particular fucsiano) se suele elegir como generadores del grupo de la monodromía los operadores M _j correspondientes a bucles, cada uno de los cuales elude solo uno de los polos del sistema en sentido antihorario. Si los índices j se eligen de tal manera que aumenten de 1 ap + 1 cuando se elude el punto base en el sentido de las agujas del reloj, entonces la única relación entre los generadores es la igualdad. ${\ Displaystyle M_ {1} \ cdots M_ {p + 1} = \ operatorname {id}}$ . El problema de Deligne-Simpson es el siguiente problema de realización: ¿Para qué tuplas de clases de conjugación en GL ( n , C ) existen tuplas irreductibles de matrices M _j de estas clases que satisfacen la relación anterior? El problema ha sido formulado por Pierre Deligne y Carlos Simpson fue el primero en obtener resultados para su resolución. Vladimir Kostov ha formulado y explorado una versión aditiva del problema de los residuos de los sistemas fucsianos . El problema también ha sido considerado por otros autores para grupos de matrices distintos de GL ( n , C ). ^[2]

Aspectos topológicos y geométricos

En el caso de un mapa de cobertura, lo vemos como un caso especial de una fibración y usamos la propiedad de elevación de homotopía para "seguir" caminos en el espacio base X (asumimos que está conectado por camino para simplificar) a medida que se levantan. arriba en la cubierta C . Si seguimos alrededor de un bucle basado en x en X , que levantamos para comenzar en c sobre x , terminaremos en algún c * nuevamente por encima de x ; es muy posible que c ≠ c * , y para codificar este se considera la acción del grupo fundamental $π$ ₁( X , x ) como un grupo de permutación en el conjunto de todo c , como un grupo de monodromía en este contexto.

En geometría diferencial, el transporte paralelo juega un papel análogo . En un haz principal B sobre un colector liso M , una conexión permite el movimiento "horizontal" de las fibras por encima de m en M a las adyacentes. El efecto, cuando se aplica a bucles basados en m, es definir un grupo holonómico de traslaciones de la fibra en m ; si el grupo de estructura de B es G , es un subgrupo de G que mide la desviación de B del paquete de productos M × G.

Grupóide monodromía y foliaciones

Un camino en la base tiene caminos en el espacio total que lo levanta. Empujar a lo largo de estos caminos da la acción monodromía del grupoide fundamental.

De manera análoga al grupoide fundamental , es posible deshacerse de la elección de un punto base y definir un grupoide monodromía. Aquí consideramos (clases de homotopía de) elevaciones de caminos en el espacio base X de una fibración ${\ Displaystyle p: {\ tilde {X}} \ to X}$ . El resultado tiene la estructura de un groupoid sobre el espacio base X . La ventaja es que podemos dejar caer el estado de conexión de X .

Además, la construcción también se puede generalizar a foliaciones : considere ${\ Displaystyle (M, {\ mathcal {F}})}$ una (posiblemente singular) foliación de M . Entonces, por cada camino en una hoja de ${\ Displaystyle {\ mathcal {F}}}$ podemos considerar su difeomorfismo inducido en secciones transversales locales a través de los puntos finales. Dentro de un gráfico simplemente conectado, este difeomorfismo se vuelve único y especialmente canónico entre diferentes secciones transversales si pasamos al germen del difeomorfismo alrededor de los puntos finales. De esta manera, también se vuelve independiente de la ruta (entre puntos finales fijos) dentro de un gráfico simplemente conectado y, por lo tanto, es invariante bajo homotopía.

Definición a través de la teoría de Galois

Sea F ( x ) el campo de las funciones racionales en la variable x sobre el campo F , que es el campo de fracciones del anillo polinomial F [ x ]. Un elemento y = f ( x ) de F ( x ) determina una extensión de campo finito [ F ( x ): F ( y )].

Esta extensión generalmente no es de Galois pero tiene el cierre de Galois L ( f ). El grupo de Galois asociado de la extensión [ L ( f ): F ( y )] se denomina grupo de monodromía de f .

En el caso de F = C , entra la teoría de la superficie de Riemann y permite la interpretación geométrica dada anteriormente. En el caso de que la extensión [ C ( x ): C ( y )] ya sea Galois, el grupo de monodromía asociado a veces se denomina grupo de transformaciones de cubierta .

Esto tiene conexiones con la teoría de Galois de cubrir espacios que conducen al teorema de existencia de Riemann .

Ver también

Grupo de trenzas
Teorema de la monodromía
Grupo de clase de mapeo (de un disco perforado)

Notas

^ König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes - Aspectos de su vida y obra (en alemán). Springer-Verlag. págs. 200–201. ISBN 9783658106195. Consultado el 5 de octubre de 2017 .
^ VP Kostov (2004), "El problema de Deligne-Simpson - una encuesta", J. Algebra , 281 (1): 83-108, arXiv : math / 0206298 , doi : 10.1016 / j.jalgebra.2004.07.013 , MR 2091962 , S2CID 119634752 y las referencias en el mismo.

Referencias

VI Danilov (2001) [1994], "Monodromy" , Encyclopedia of Mathematics , EMS Press
"Group-groupoids y groupoids monodromy", O. Mucuk, B. Kılıçarslan, T. ¸Sahan, N. Alemdar, Topology and its Applications 158 (2011) 2034–2042 doi: 10.1016 / j.topol.2011.06.048
R. Brown Topología y Groupoids (2006).
PJ Higgins, "Categorías y grupos", van Nostrand (1971) TAC Reimpresión

[König2015-1] König, Wolfgang; Sprekels, Jürgen (2015). Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes - Aspectos de su vida y obra (en alemán). Springer-Verlag. págs. 200–201. ISBN 9783658106195. Consultado el 5 de octubre de 2017 .

[2] VP Kostov (2004), "El problema de Deligne-Simpson - una encuesta", J. Algebra , 281 (1): 83-108, arXiv : math / 0206298 , doi : 10.1016 / j.jalgebra.2004.07.013 , MR 2091962 , S2CID 119634752 y las referencias en el mismo.

[1]