Función continua

Función matemática sin cambios bruscos de valor

Parte de una serie de artículos sobre
Cálculo
Teorema fundamental Regla integral de Leibniz Límites de funciones Continuidad Teorema del valor medio Teorema de rolle
Diferencial Definiciones Derivado  ( generalizaciones ) Diferencial infinitesimal de una función total Conceptos Notación de diferenciación Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Rules and identities Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula
Integral Lists of integrals Integral transform Definitions Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integral of inverse functions Integration by Parts Discs Cylindrical shells Substitution (trigonometric, Weierstrass, Euler) Euler's formula Partial fractions Changing order Reduction formulae Differentiating under the integral sign Risch algorithm
Serie Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Gradient Green's Stokes' Divergence generalized Stokes
Multivariable Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian
Especializado Fractional Malliavin Stochastic Variations
Diverso Precalculus History Glossary List of topics Integration Bee Analysis
v t mi

En matemáticas , una función continua es una función que no tiene cambios bruscos de valor , conocidos como discontinuidades . Más precisamente, una función es continua si se pueden asegurar cambios arbitrariamente pequeños en su salida restringiendo a cambios suficientemente pequeños en su entrada. Si no es continua, se dice que una función es discontinua . Hasta el siglo XIX, los matemáticos se basaron en gran medida en nociones intuitivas de continuidad, durante las cuales se hicieron intentos como la definición épsilon-delta para formalizarla.

La continuidad de las funciones es uno de los conceptos centrales de la topología , que se trata en su totalidad a continuación. La parte introductoria de este artículo se centra en el caso especial en el que las entradas y salidas de funciones son números reales . Una forma más fuerte de continuidad es la continuidad uniforme . Además, este artículo analiza la definición para el caso más general de funciones entre dos espacios métricos . En la teoría del orden , especialmente en la teoría del dominio , se considera una noción de continuidad conocida como continuidad de Scott . Existen otras formas de continuidad, pero no se tratan en este artículo.

Como ejemplo, la función H ( t ) que denota la altura de una flor en crecimiento en el tiempo t se consideraría continua. Por el contrario, la función M ( t ) que denota la cantidad de dinero en una cuenta bancaria en el momento t se consideraría discontinua, ya que "salta" en cada momento en el que se deposita o retira dinero.

Historia

Una forma de la definición épsilon-delta de continuidad fue dada por primera vez por Bernard Bolzano en 1817. Augustin-Louis Cauchy definió la continuidad de${\displaystyle y=f(x)}$ de la siguiente manera: un incremento infinitamente pequeño ${\displaystyle \alpha }$de la variable independiente x siempre produce un cambio infinitamente pequeño${\displaystyle f(x+\alpha )-f(x)}$de la variable dependiente y (véase, por ejemplo, Cours d'Analyse , p. 34). Cauchy definió cantidades infinitamente pequeñas en términos de cantidades variables, y su definición de continuidad se asemeja mucho a la definición infinitesimal utilizada hoy (ver microcontinuidad ). La definición formal y la distinción entre continuidad puntual y continuidad uniforme fueron dadas por primera vez por Bolzano en la década de 1830, pero el trabajo no se publicó hasta la década de 1930. Al igual que Bolzano, ^[1] Karl Weierstrass ^[2] negó la continuidad de una función en un punto c a menos que estuviera definida en y en ambos lados de c , pero Édouard Goursat ^[3]permitió que la función se definiera solo en y en un lado de c , y Camille Jordan ^{[4] lo} permitió incluso si la función se definió solo en c . Las tres definiciones no equivalentes de continuidad puntual todavía están en uso. ^[5] Eduard Heine proporcionó la primera definición publicada de continuidad uniforme en 1872, pero basó estas ideas en conferencias dadas por Peter Gustav Lejeune Dirichlet en 1854. ^[6]

Funciones reales

Definición

La función ${\displaystyle f(x)={\tfrac {1}{x}}}$ es continuo en el dominio ${\displaystyle \mathbb {R} \setminus \{0\}}$, pero no es continuo en el dominio ${\displaystyle \mathbb {R} }$ porque no está definido en ${\displaystyle x=0}$

Una función real , que es una función de números reales a números reales, se puede representar mediante una gráfica en el plano cartesiano ; tal función es continua si, en términos generales, el gráfico es una única curva ininterrumpida cuyo dominio es la línea real completa. A continuación se ofrece una definición más rigurosa matemáticamente. ^[7]

En un primer curso de cálculo se suele dar una definición rigurosa de la continuidad de las funciones reales en términos de la idea de límite . Primero, se dice que una función f con variable x es continua en el punto c de la línea real, si el límite de${\displaystyle f(x),}$cuando x se acerca a ese punto c , es igual al valor${\displaystyle f(c)}$; y segundo, se dice que la función (como un todo) es continua , si es continua en todos los puntos. Se dice que una función es discontinua (o que tiene una discontinuidad ) en algún momento cuando no es continua allí. Estos puntos en sí mismos también se tratan como discontinuidades .

Hay varias definiciones diferentes de continuidad de una función. A veces se dice que una función es continua si es continua en todos los puntos de su dominio. En este caso, la función${\displaystyle f(x)=\tan(x),}$ con el dominio de todo lo real ${\displaystyle x\neq \pi {\frac {2n+1}{2}},}$ ${\displaystyle n}$cualquier entero, es continuo. A veces se hace una excepción para los límites del dominio. Por ejemplo, la gráfica de la función${\displaystyle f(x)={\sqrt {x}},}$con el dominio de todos los reales no negativos, tiene un extremo izquierdo . En este caso, solo se requiere el límite de la derecha para igualar el valor de la función. Bajo esta definición f es continua en el límite${\displaystyle x=0}$y así para todos los argumentos no negativos. La definición más común y restrictiva es que una función es continua si es continua en todos los números reales. En este caso, los dos ejemplos anteriores no son continuos, pero cada función polinomial es continua, al igual que las funciones seno , coseno y exponencial . Se debe tener cuidado al usar la palabra continuo , de modo que quede claro en el contexto qué significado de la palabra se pretende.

Usando la notación matemática, hay varias formas de definir funciones continuas en cada uno de los tres sentidos mencionados anteriormente.

Dejar

${\displaystyle f:D\to \mathbb {R} \quad }$ser una función definida en un subconjunto ${\displaystyle D}$ del set ${\displaystyle \mathbb {R} }$ de números reales.

Este subconjunto ${\displaystyle D}$es el dominio de f . Algunas opciones posibles incluyen

${\displaystyle D=\mathbb {R} \quad }$ (${\displaystyle D}$es todo el conjunto de números reales), o, para una y b números reales,

${\displaystyle D=[a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}\quad }$ (${\displaystyle D}$es un intervalo cerrado ), o

${\displaystyle D=(a,b)=\{x\in \mathbb {R} \mid a<x<b\}\quad }$ (${\displaystyle D}$es un intervalo abierto ).

En el caso del dominio ${\displaystyle D}$ definiéndose como un intervalo abierto, ${\displaystyle a}$ y ${\displaystyle b}$ no perteneces a ${\displaystyle D}$, y los valores de ${\displaystyle f(a)}$ y ${\displaystyle f(b)}$ no importa para la continuidad en ${\displaystyle D}$.

Definición en términos de límites de funciones

La función f es continua en algún punto c de su dominio si el límite de${\displaystyle f(x),}$cuando x se acerca a c a través del dominio de f , existe y es igual a${\displaystyle f(c).}$^[8] En notación matemática, esto se escribe como

$${\displaystyle \lim _{x\to c}{f(x)}=f(c).}$$

En detalle, esto significa tres condiciones: primero, f debe definirse en c (garantizado por el requisito de que c esté en el dominio de f ). En segundo lugar, tiene que existir el límite en el lado izquierdo de esa ecuación. En tercer lugar, el valor de este límite debe ser igual a${\displaystyle f(c).}$

(Aquí, hemos asumido que el dominio de f no tiene puntos aislados ).

Definición en términos de barrios

Una vecindad de un punto c es un conjunto que contiene, al menos, todos los puntos dentro de una distancia fija de c . Intuitivamente, una función es continua en un punto c si el rango de f sobre la vecindad de c se reduce a un solo punto${\displaystyle f(c)}$a medida que el ancho de la vecindad alrededor de c se reduce a cero. Más precisamente, una función f es continua en un punto c de su dominio si, para cualquier vecindad${\displaystyle N_{1}(f(c))}$ hay un barrio ${\displaystyle N_{2}(c)}$ en su dominio tal que ${\displaystyle f(x)\in N_{1}(f(c))}$ cuando sea ${\displaystyle x\in N_{2}(c).}$

Esta definición solo requiere que el dominio y el codominio sean espacios topológicos y, por lo tanto, es la definición más general. De esta definición se deduce que una función f es automáticamente continua en cada punto aislado de su dominio. Como ejemplo específico, cada función de valor real en el conjunto de números enteros es continua.

Definición en términos de límites de secuencias

La secuencia ${\displaystyle \exp(1/n)}$ converge a exp (0)

En cambio, se puede requerir que para cualquier secuencia ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$de puntos en el dominio que converge a c , la secuencia correspondiente${\displaystyle \left(f(x_{n})\right)_{n\in \mathbb {N} }}$ converge a ${\displaystyle f(c).}$ En notación matemática, ${\displaystyle \forall (x_{n})_{n\in \mathbb {N} }\subset D:\lim _{n\to \infty }x_{n}=c\Rightarrow \lim _{n\to \infty }f(x_{n})=f(c)\,.}$

Definiciones de Weierstrass y Jordan (épsilon-delta) de funciones continuas

Ilustración de la ${\displaystyle \varepsilon -\delta }$-definición: para ${\displaystyle \varepsilon =0.5,c=2,}$ el valor ${\displaystyle \delta =0.5}$ satisface la condición de la definición.

Incluyendo explícitamente la definición del límite de una función, obtenemos una definición autocontenida: Dada una función ${\displaystyle f:D\to R}$ como arriba y un elemento ${\displaystyle x_{0}}$del dominio D , se dice que f es continua en el punto${\displaystyle x_{0}}$ cuando se cumple lo siguiente: Para cualquier número ${\displaystyle \varepsilon >0,}$ por pequeño que sea, existe un número ${\displaystyle \delta >0}$tal que para todo x en el dominio de f con${\displaystyle x_{0}-\delta <x<x_{0}+\delta ,}$ El valor de ${\displaystyle f(x)}$ satisface

$${\displaystyle f\left(x_{0}\right)-\varepsilon <f(x)<f(x_{0})+\varepsilon .}$$

Escrito alternativamente, continuidad de ${\displaystyle f:D\to R}$ a ${\displaystyle x_{0}\in D}$ significa que para cada ${\displaystyle \varepsilon >0,}$ existe un ${\displaystyle \delta >0}$ tal que para todos ${\displaystyle x\in D}$:

$${\displaystyle \left|x-x_{0}\right|<\delta {\text{ implies }}|f(x)-f(x_{0})|<\varepsilon .}$$

De manera más intuitiva, podemos decir que si queremos obtener todos los ${\displaystyle f(x)}$valores para quedarse en algún pequeño vecindario alrededor${\displaystyle f\left(x_{0}\right),}$simplemente tenemos que elegir un vecindario lo suficientemente pequeño para los valores de x alrededor${\displaystyle x_{0}.}$ Si podemos hacer eso, no importa cuán pequeño sea el ${\displaystyle f(x)}$vecindario es, entonces f es continua en${\displaystyle x_{0}.}$

En términos modernos, esto se generaliza mediante la definición de continuidad de una función con respecto a una base para la topología , aquí la topología métrica .

Weierstrass había requerido que el intervalo ${\displaystyle x_{0}-\delta <x<x_{0}+\delta }$estar completamente dentro del dominio D , pero Jordan eliminó esa restricción.

Definición en términos de control del resto

En las pruebas y el análisis numérico, a menudo necesitamos saber qué tan rápido están convergiendo los límites, o en otras palabras, el control del resto. Podemos formalizar esto en una definición de continuidad. Una función${\displaystyle C:[0,\infty )\to [0,\infty ]}$ se llama función de control si

• C no es decreciente
• ${\displaystyle \inf _{\delta >0}C(\delta )=0}$

Una función ${\displaystyle f:D\to R}$es C -continuo en${\displaystyle x_{0}}$ Si

$${\displaystyle |f(x)-f(x_{0})|\leq C\left(\left|x-x_{0}\right|\right){\text{ for all }}x\in D}$$

Una función es continua en ${\displaystyle x_{0}}$si es C -Continua para alguna función de control C .

Este enfoque conduce naturalmente a refinar la noción de continuidad al restringir el conjunto de funciones de control admisibles. Para un conjunto dado de funciones de control${\displaystyle {\mathcal {C}}}$ una función es ${\displaystyle {\mathcal {C}}}$-continuo si es ${\displaystyle C}$-continuo para algunos ${\displaystyle C\in {\mathcal {C}}.}$Por ejemplo, las funciones continuas de Lipschitz y Hölder del exponente α a continuación están definidas por el conjunto de funciones de control

$${\displaystyle {\mathcal {C}}_{\mathrm {Lipschitz} }=\{C:C(\delta )=K|\delta |,\ K>0\}}$$

respectivamente

$${\displaystyle {\mathcal {C}}_{{\text{Hölder}}-\alpha }=\{C:C(\delta )=K|\delta |^{\alpha },\ K>0\}.}$$

Definición mediante oscilación

La falla de una función para ser continua en un punto se cuantifica por su oscilación .

La continuidad también se puede definir en términos de oscilación : una función f es continua en un punto${\displaystyle x_{0}}$si y solo si su oscilación en ese punto es cero; ^[9] en símbolos,${\displaystyle \omega _{f}(x_{0})=0.}$Una ventaja de esta definición es que cuantifica la discontinuidad: la oscilación da forma tanto la función es discontinua en un punto.

Esta definición es útil en la teoría descriptiva de conjuntos para estudiar el conjunto de discontinuidades y puntos continuos; los puntos continuos son la intersección de los conjuntos donde la oscilación es menor que${\displaystyle \varepsilon }$ (de ahí un G δ {\ Displaystyle G _ {\ delta}} set ) - y da una prueba muy rápida de una dirección de la condición de integrabilidad de Lebesgue . ^[10]

La oscilación es equivalente a la ${\displaystyle \varepsilon -\delta }$definición mediante una simple reorganización, y mediante el uso de un límite ( lim sup , lim inf ) para definir la oscilación: si (en un punto dado) para un determinado${\displaystyle \varepsilon _{0}}$ no hay ${\displaystyle \delta }$ que satisface el ${\displaystyle \varepsilon -\delta }$ definición, entonces la oscilación es al menos ${\displaystyle \varepsilon _{0},}$ y viceversa si por cada ${\displaystyle \varepsilon }$ hay un deseado ${\displaystyle \delta ,}$ la oscilación es 0. La definición de oscilación se puede generalizar naturalmente a mapas de un espacio topológico a un espacio métrico.

Definición usando los hiperrealistas

Cauchy definió la continuidad de una función en los siguientes términos intuitivos: un cambio infinitesimal en la variable independiente corresponde a un cambio infinitesimal de la variable dependiente (ver Cours d'analyse , página 34). El análisis no estándar es una forma de hacer esto matemáticamente riguroso. La línea real se aumenta mediante la adición de números infinitos e infinitesimales para formar los números hiperreales . En el análisis no estándar, la continuidad se puede definir de la siguiente manera.

Una función f de valor real es continua en x si su extensión natural a los hiperreal tiene la propiedad de que para todo dx infinitesimal ,${\displaystyle f(x+dx)-f(x)}$es infinitesimal ^[11]

(ver microcontinuidad ). En otras palabras, un incremento infinitesimal de la variable independiente siempre produce un cambio infinitesimal de la variable dependiente, dando una expresión moderna a la definición de continuidad de Augustin-Louis Cauchy .

Construcción de funciones continuas

La gráfica de una función cúbica no tiene saltos ni huecos. La función es continua.

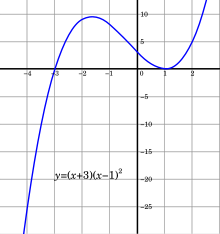
La verificación de la continuidad de una función dada se puede simplificar al verificar una de las propiedades definitorias anteriores para los bloques de construcción de la función dada. Es sencillo demostrar que la suma de dos funciones, continua en algún dominio, también es continua en este dominio. Dado

$${\displaystyle f,g\colon D\to \mathbb {R} ,}$$

entonces la suma de funciones continuas

$${\displaystyle s=f+g}$$

(definido por ${\displaystyle s(x)=f(x)+g(x)}$ para todos ${\displaystyle x\in D}$) es continuo en ${\displaystyle D.}$

Lo mismo vale para el producto de funciones continuas ,

$${\displaystyle p=f\cdot g}$$

(definido por ${\displaystyle p(x)=f(x)\cdot g(x)}$ para todos ${\displaystyle x\in D}$) es continuo en ${\displaystyle D.}$

Combinando las preservaciones anteriores de la continuidad y la continuidad de las funciones constantes y de la función de identidad ${\displaystyle I(x)=x}$ en ${\displaystyle \mathbb {R} }$, se llega a la continuidad de todas las funciones polinomiales en${\displaystyle \mathbb {R} }$, como

$${\displaystyle f(x)=x^{3}+x^{2}-5x+3}$$

(en la foto de la derecha).

La gráfica de una función racional continua . La función no está definida para${\displaystyle x=-2.}$Las líneas verticales y horizontales son asíntotas .

De la misma manera se puede demostrar que el recíproco de una función continua

$${\displaystyle r=1/f}$$

(definido por ${\displaystyle r(x)=1/f(x)}$ para todos ${\displaystyle x\in D}$ tal que ${\displaystyle f(x)\neq 0}$) es continuo en ${\displaystyle D\setminus \{x:f(x)=0\}.}$

Esto implica que, excluyendo las raíces de ${\displaystyle g,}$el cociente de funciones continuas

$${\displaystyle q=f/g}$$

(definido por ${\displaystyle q(x)=f(x)/g(x)}$ para todos ${\displaystyle x\in D}$, tal que ${\displaystyle g(x)\neq 0}$) también es continuo en ${\displaystyle D\setminus \{x:g(x)=0\}}$.

Por ejemplo, la función (en la imagen)

$${\displaystyle y(x)={\frac {2x-1}{x+2}}}$$

está definido para todos los números reales ${\displaystyle x\neq -2}$y es continuo en cada uno de esos puntos. Por tanto, es una función continua. La cuestión de la continuidad en${\displaystyle x=-2}$ no surge, ya que ${\displaystyle x=-2}$ no está en el dominio de ${\displaystyle y.}$ No hay función continua ${\displaystyle F:\mathbb {R} \to \mathbb {R} }$ eso concuerda con ${\displaystyle y(x)}$ para todos ${\displaystyle x\neq -2.}$

Las funciones sinc y cos

Dado que la función seno es continua en todos los reales, la función sinc ${\displaystyle G(x)=\sin(x)/x,}$ es definido y continuo para todos los reales ${\displaystyle x\neq 0.}$Sin embargo, a diferencia del ejemplo anterior, G se puede extender a una función continua en todos los números reales, definiendo el valor${\displaystyle G(0)}$ ser 1, que es el límite de ${\displaystyle G(x),}$cuando x se acerca a 0, es decir,

$${\displaystyle G(0)=\lim _{x\to 0}{\frac {\sin x}{x}}=1.}$$

Por lo tanto, estableciendo

${\displaystyle G(x)={\begin{cases}{\frac {\sin(x)}{x}}&{\text{ if }}x\neq 0\\1&{\text{ if }}x=0,\end{cases}}}$

la función sinc se convierte en una función continua en todos los números reales. El término singularidad removible se usa en tales casos, cuando (re) definir valores de una función para que coincidan con los límites apropiados hacen que una función sea continua en puntos específicos.

Una construcción más complicada de funciones continuas es la composición de funciones . Dadas dos funciones continuas

$${\displaystyle g:D_{g}\subseteq \mathbb {R} \to R_{g}\subseteq \mathbb {R} \quad {\text{ and }}\quad f:D_{f}\subseteq \mathbb {R} \to R_{f}\subseteq D_{g},}$$

su composición, denotada como${\displaystyle c=g\circ f:D_{f}\to \mathbb {R} ,}$ y definido por ${\displaystyle c(x)=g(f(x)),}$ es continuo.

Esta construcción permite afirmar, por ejemplo, que

$${\displaystyle e^{\sin(\ln x)}}$$

es continuo para todos ${\displaystyle x>0.}$

Ejemplos de funciones discontinuas

Gráfico de la función signum. Muestra que${\displaystyle \lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)\neq \operatorname {sgn} \left(\lim _{n\to \infty }{\tfrac {1}{n}}\right)}$. Por tanto, la función signum es discontinua en 0 (ver sección 2.1.3 ).

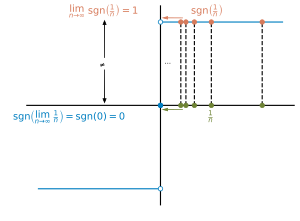
Un ejemplo de una función discontinua es la función escalón Heaviside ${\displaystyle H}$, definido por

${\displaystyle H(x)={\begin{cases}1&{\text{ if }}x\geq 0\\0&{\text{ if }}x<0\end{cases}}}$

Elige por ejemplo ${\displaystyle \varepsilon =1/2}$. Entonces no hay${\displaystyle \delta }$-barrio alrededor${\displaystyle x=0}$, es decir, sin intervalo abierto ${\displaystyle (-\delta ,\;\delta )}$ con ${\displaystyle \delta >0,}$ que forzará a todos los ${\displaystyle H(x)}$ valores para estar dentro del ${\displaystyle \varepsilon }$-barrio de${\displaystyle H(0)}$, es decir, dentro ${\displaystyle (1/2,\;3/2)}$. Intuitivamente podemos pensar en este tipo de discontinuidad como un salto repentino en los valores de las funciones.

Del mismo modo, la función signum o sign

${\displaystyle \operatorname {sgn}(x)={\begin{cases}\;\;\ 1&{\text{ if }}x>0\\\;\;\ 0&{\text{ if }}x=0\\-1&{\text{ if }}x<0\end{cases}}}$

es discontinuo en ${\displaystyle x=0}$pero continuo en todas partes. Otro ejemplo más: la función

${\displaystyle f(x)={\begin{cases}\sin \left(x^{-2}\right)&{\text{ if }}x\neq 0\\0&{\text{ if }}x=0\end{cases}}}$

es continuo en todas partes excepto en ${\displaystyle x=0}$.

Gráfico de puntos de la función de Thomae en el intervalo (0,1). El punto más alto en el medio muestra f (1/2) = 1/2.

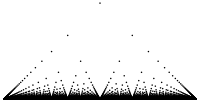
Además de las continuidades y discontinuidades plausibles como las anteriores, también hay funciones con un comportamiento, a menudo acuñado como patológico , por ejemplo, la función de Thomae ,

${\displaystyle f(x)={\begin{cases}1&{\text{ if }}x=0\\{\frac {1}{q}}&{\text{ if }}x={\frac {p}{q}}{\text{(in lowest terms) is a rational number}}\\0&{\text{ if }}x{\text{ is irrational}}.\end{cases}}}$

es continuo en todos los números irracionales y discontinuo en todos los números racionales. De manera similar, la función de Dirichlet , la función indicadora para el conjunto de números racionales,

${\displaystyle D(x)={\begin{cases}0&{\text{ if }}x{\text{ is irrational }}(\in \mathbb {R} \setminus \mathbb {Q} )\\1&{\text{ if }}x{\text{ is rational }}(\in \mathbb {Q} )\end{cases}}}$

no es continuo en ninguna parte.

Propiedades

Un lema útil

Dejar ${\displaystyle f(x)}$ ser una función que es continua en un punto ${\displaystyle x_{0},}$ y ${\displaystyle y_{0}}$ ser un valor como ${\displaystyle f\left(x_{0}\right)\neq y_{0}.}$ Luego ${\displaystyle f(x)\neq y_{0}}$ a lo largo de algún barrio de ${\displaystyle x_{0}.}$^[12]

Prueba: según la definición de continuidad, tome${\displaystyle \varepsilon ={\frac {|y_{0}-f(x_{0})|}{2}}>0}$ , entonces existe ${\displaystyle \delta >0}$ tal que

$${\displaystyle \left|f(x)-f(x_{0})\right|<{\frac {\left|y_{0}-f(x_{0})\right|}{2}}\quad {\text{ whenever }}\quad |x-x_{0}|<\delta }$$

Suponga que hay un punto en el vecindario ${\displaystyle |x-x_{0}|<\delta }$ para cual ${\displaystyle f(x)=y_{0};}$ entonces tenemos la contradicción

$${\displaystyle \left|f(x_{0})-y_{0}\right|<{\frac {\left|f(x_{0})-y_{0}\right|}{2}}.}$$

Teorema del valor intermedio

El teorema del valor intermedio es un teorema de existencia , basado en la propiedad de completitud del número real , y establece:

Si la función de valor real f es continua en el intervalo cerrado ${\displaystyle [a,b],}$y k es un número entre${\displaystyle f(a)}$ y ${\displaystyle f(b),}$ entonces hay un numero ${\displaystyle c\in [a,b],}$ tal que ${\displaystyle f(x)=k.}$

Por ejemplo, si un niño crece de 1 ma 1,5 m entre las edades de dos y seis años, entonces, en algún momento entre los dos y los seis años, la altura del niño debe haber sido de 1,25 m.

Como consecuencia, si f es continua en${\displaystyle [a,b]}$ y ${\displaystyle f(a)}$ y ${\displaystyle f(b)}$difieren en el signo , entonces, en algún momento${\displaystyle c\in [a,b],}$ ${\displaystyle f(c)}$debe ser igual a cero .

Teorema del valor extremo

El teorema del valor extremo establece que si una función f se define en un intervalo cerrado${\displaystyle [a,b]}$ (o cualquier conjunto cerrado y acotado) y es continua allí, entonces la función alcanza su máximo, es decir, existe ${\displaystyle c\in [a,b]}$ con ${\displaystyle f(c)\geq f(x)}$ para todos ${\displaystyle x\in [a,b].}$Lo mismo ocurre con el mínimo de f . Estas afirmaciones no son, en general, verdaderas si la función se define en un intervalo abierto${\displaystyle (a,b)}$ (o cualquier conjunto que no sea a la vez cerrado y acotado), como, por ejemplo, la función continua ${\displaystyle f(x)={\frac {1}{x}},}$ definido en el intervalo abierto (0,1), no alcanza un máximo, siendo ilimitado por encima.

Relación con la diferenciabilidad y la integrabilidad

Cada función diferenciable

$${\displaystyle f:(a,b)\to \mathbb {R} }$$

es continuo, como se puede demostrar. Lo contrario no se cumple: por ejemplo, la función de valor absoluto

${\displaystyle f(x)=|x|={\begin{cases}\;\;\ x&{\text{ if }}x\geq 0\\-x&{\text{ if }}x<0\end{cases}}}$

es continuo en todas partes. Sin embargo, no es diferenciable en${\displaystyle x=0}$(pero es así en todas partes). La función de Weierstrass también es continua en todas partes, pero no diferenciable en ninguna parte.

La derivada ${\displaystyle f(x)}$de una función diferenciable f ( x ) no necesita ser continua. Si f ′ ( x ) es continua, se dice que f ( x ) es continuamente diferenciable. El conjunto de tales funciones se denota${\displaystyle C^{1}((1,b)).}$ De manera más general, el conjunto de funciones

$${\displaystyle f:\Omega \to \mathbb {R} }$$

(de un intervalo abierto (o subconjunto abierto de${\displaystyle \mathbb {R} }$) ${\displaystyle \Omega }$a los reales) tal que f es${\displaystyle n}$ veces diferenciable y tal que el ${\displaystyle n}$-ésima derivada de f es continua se denota${\displaystyle C^{n}(\Omega ).}$Ver clase de diferenciabilidad . En el campo de la infografía, las propiedades relacionadas (pero no idénticas) con${\displaystyle C^{0},C^{1},C^{2}}$ a veces se les llama ${\displaystyle G^{0}}$ (continuidad de cargo), ${\displaystyle G^{1}}$ (continuidad de tangencia), y ${\displaystyle G^{2}}$(continuidad de curvatura); consulte Suavidad de curvas y superficies .

Cada función continua

$${\displaystyle f:[a,b]\to \mathbb {R} }$$

es integrable (por ejemplo, en el sentido de la integral de Riemann ). Lo contrario no se cumple, como muestra la función de signo (integrable, pero discontinua) .

Límites puntuales y uniformes

Una secuencia de funciones continuas ${\displaystyle f_{n}(x)}$ cuya función límite (puntual) ${\displaystyle f(x)}$es discontinuo. La convergencia no es uniforme.

Dada una secuencia

$${\displaystyle f_{1},f_{2},\dotsc :I\to \mathbb {R} }$$

de funciones tales que el límite

$${\displaystyle f(x):=\lim _{n\to \infty }f_{n}(x)}$$

existe para todos ${\displaystyle x\in D,}$, la función resultante ${\displaystyle f(x)}$se conoce como el límite puntual de la secuencia de funciones ${\displaystyle \left(f_{n}\right)_{n\in N}.}$ La función de límite puntual no necesita ser continua, incluso si todas las funciones ${\displaystyle f_{n}}$son continuos, como muestra la animación de la derecha. Sin embargo, f es continua si todas las funciones${\displaystyle f_{n}}$son continuas y la secuencia converge uniformemente , según el teorema de convergencia uniforme . Este teorema se puede utilizar para demostrar que las funciones exponenciales , los logaritmos , la función raíz cuadrada y las funciones trigonométricas son continuas.

Direccional y semicontinuidad

• 

  Una función continua a la derecha

• 

  Una función continua a la izquierda

Las funciones discontinuas pueden ser discontinuas de forma restringida, dando lugar al concepto de continuidad direccional (o funciones continuas derecha e izquierda) y semicontinuidad . En términos generales, una función es continua a la derecha si no se produce ningún salto cuando se llega al punto límite desde la derecha. Formalmente, se dice que f es continua a la derecha en el punto c si se cumple lo siguiente: Para cualquier número${\displaystyle \varepsilon >0}$ por pequeño que sea, existe un número ${\displaystyle \delta >0}$tal que para todo x en el dominio con${\displaystyle c<x<c+\delta ,}$ El valor de ${\displaystyle f(x)}$ satisfará

$${\displaystyle |f(x)-f(c)|<\varepsilon .}$$

Esta es la misma condición que para las funciones continuas, excepto que se requiere mantener para x estrictamente mayor que c solamente. Requiriéndolo en su lugar para todo x con${\displaystyle c-\delta <x<c}$produce la noción de funciones continuas a la izquierda . Una función es continua si y solo si es tanto continua a la derecha como continua a la izquierda.

Una función f es semicontinua más baja si, aproximadamente, los saltos que puedan ocurrir solo van hacia abajo, pero no hacia arriba. Es decir, para cualquier${\displaystyle \varepsilon >0,}$ existe un numero ${\displaystyle \delta >0}$tal que para todo x en el dominio con${\displaystyle |x-c|<\delta ,}$ El valor de ${\displaystyle f(x)}$ satisface

$${\displaystyle f(x)\geq f(c)-\epsilon .}$$

La condición inversa es la semicontinuidad superior .

Funciones continuas entre espacios métricos

El concepto de funciones continuas de valor real se puede generalizar a funciones entre espacios métricos . Un espacio métrico es un conjunto X equipado con una función (llamada métrica )${\displaystyle d_{X},}$que puede ser pensado como una medida de la distancia de cualesquiera dos elementos en X . Formalmente, la métrica es una función

$${\displaystyle d_{X}:X\times X\to \mathbb {R} }$$

que satisface una serie de requisitos, en particular la desigualdad del triángulo . Dados dos espacios métricos${\displaystyle \left(X,d_{X}\right)}$ y ${\displaystyle \left(Y,d_{Y}\right)}$ y una función

$${\displaystyle f:X\to Y}$$

entonces f es continua en el punto${\displaystyle c\in X}$ (con respecto a las métricas dadas) si para cualquier número real positivo ${\displaystyle \varepsilon >0,}$ existe un número real positivo ${\displaystyle \delta >0}$ tal que todos ${\displaystyle x\in X}$ satisfactorio ${\displaystyle d_{X}(x,c)<\delta }$ también satisfará ${\displaystyle d_{Y}(f(x),f(c))<\varepsilon .}$ Como en el caso de las funciones reales anteriores, esto es equivalente a la condición de que para cada secuencia ${\displaystyle \left(x_{n}\right)}$en X con límite${\displaystyle \lim x_{n}=c,}$ tenemos ${\displaystyle \lim f\left(x_{n}\right)=f(c).}$La última condición se puede debilitar de la siguiente manera: f es continua en el punto c si y solo si para cada secuencia convergente${\displaystyle \left(x_{n}\right)}$en X con límite c , la secuencia${\displaystyle \left(f\left(x_{n}\right)\right)}$es una secuencia de Cauchy y c está en el dominio de f .

El conjunto de puntos en los que una función entre espacios métricos es continua es un G δ {\ Displaystyle G _ {\ delta}} conjunto  - esto se sigue de la${\displaystyle \varepsilon -\delta }$ definición de continuidad.

Esta noción de continuidad se aplica, por ejemplo, en el análisis funcional . Una declaración clave en esta área dice que un operador lineal

$${\displaystyle T:V\to W}$$

entre los espacios vectoriales normativos V y W (que son espacios vectoriales equipados con una norma compatible , denotada${\displaystyle \|x\|}$) es continuo si y solo si está acotado , es decir, hay una constante K tal que

$${\displaystyle \|T(x)\|\leq K\|x\|}$$

para todos ${\displaystyle x\in V.}$

Continuidad uniforme, Hölder y Lipschitz

Para una función continua de Lipschitz, hay un cono doble (mostrado en blanco) cuyo vértice se puede trasladar a lo largo del gráfico, de modo que el gráfico siempre permanece completamente fuera del cono.

El concepto de continuidad de funciones entre espacios métricos se puede fortalecer de diversas formas limitando la forma ${\displaystyle \delta }$ depende de ${\displaystyle \varepsilon }$y c en la definición anterior. Intuitivamente, una función f como la anterior es uniformemente continua si el${\displaystyle \delta }$no depende del punto c . Más precisamente, se requiere que para cada número real ${\displaystyle \varepsilon >0}$ existe ${\displaystyle \delta >0}$ tal que por cada ${\displaystyle c,b\in X}$ con ${\displaystyle d_{X}(b,c)<\delta ,}$ tenemos eso ${\displaystyle d_{Y}(f(b),f(c))<\varepsilon .}$Por tanto, cualquier función uniformemente continua es continua. Lo contrario no se cumple en general, pero sí cuando el espacio de dominio X es compacto . Los mapas uniformemente continuos se pueden definir en la situación más general de espacios uniformes . ^[13]

Una función es Hölder continua con exponente α (un número real) si hay una constante K tal que para todos${\displaystyle b,c\in X,}$ la desigualdad

$${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot (d_{X}(b,c))^{\alpha }}$$

sostiene. Cualquier función continua de Hölder es uniformemente continua. El caso particular${\displaystyle \alpha =1}$se conoce como continuidad de Lipschitz . Es decir, una función es continua de Lipschitz si hay una constante K tal que la desigualdad

$${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot d_{X}(b,c)}$$

se sostiene para cualquier ${\displaystyle b,c\in X.}$^[14] La condición de Lipschitz ocurre, por ejemplo, en el teorema de Picard-Lindelöf relativo a las soluciones de ecuaciones diferenciales ordinarias .

Funciones continuas entre espacios topológicos

Otra noción de continuidad, más abstracta, es la continuidad de funciones entre espacios topológicos en los que generalmente no existe una noción formal de distancia, como ocurre en el caso de los espacios métricos . Un espacio topológico es un conjunto X junto con una topología en X , que es un conjunto de subconjuntos de X que satisfacen algunos requisitos con respecto a sus uniones e intersecciones que generalizan las propiedades de las bolas abiertas en espacios métricos al tiempo que permiten hablar sobre los vecindarios de un punto dado. Los elementos de una topología se denominan subconjuntos abiertos de X (con respecto a la topología).

Una función

$${\displaystyle f:X\to Y}$$

entre dos espacios topológicos X e Y es continuo si para cada conjunto abierto${\displaystyle V\subseteq Y,}$la imagen inversa

$${\displaystyle f^{-1}(V)=\{x\in X\;|\;f(x)\in V\}}$$

es un subconjunto abierto de X . Es decir, f es una función entre los conjuntos X e Y (no sobre los elementos de la topología${\displaystyle T_{X}}$), Pero la continuidad de f depende de las topologías utilizadas en X y Y .

Esto es equivalente a la condición de que los preimages de los conjuntos cerrados (que son los complementos de los subconjuntos abiertos) en Y están cerrados en X .

Un ejemplo extremo: si a un conjunto X se le da la topología discreta (en la que cada subconjunto está abierto), todas las funciones

$${\displaystyle f:X\to T}$$

a cualquier espacio topológico T son continuas. Por otro lado, si X está equipado con la topología indiscreta (en la que los únicos subconjuntos abiertos son el conjunto vacío y X ) y el espacio T conjunto es al menos T 0 , entonces las únicas funciones continuas son las funciones constantes. Por el contrario, cualquier función cuyo alcance sea indiscreto es continua.

Continuidad en un punto

Continuidad en un punto: para cada vecindario V de${\displaystyle f(x),}$, hay una vecindad U de x tal que${\displaystyle f(U)\subseteq V}$

La traducción al idioma de los barrios del ( ε , δ ) {\ Displaystyle (\ varepsilon, \ delta)} -la definición de continuidad conduce a la siguiente definición de la continuidad en un punto:

Una función ${\displaystyle f:X\to Y}$ es continuo en un punto ${\displaystyle x\in X}$si y solo si para cualquier vecindario V de${\displaystyle f(x)}$en Y , hay una vecindad U de x tal que${\displaystyle f(U)\subseteq V.}$

Esta definición es equivalente a la misma declaración con vecindarios restringidos a vecindarios abiertos y puede reformularse de varias maneras usando preimágenes en lugar de imágenes.

Además, como todo conjunto que contiene un barrio es también un barrio, y ${\displaystyle f^{-1}(V)}$es el subconjunto más grande U de X tal que${\displaystyle f(U)\subseteq V,}$ esta definición se puede simplificar en:

Una función ${\displaystyle f:X\to Y}$ es continuo en un punto ${\displaystyle x\in X}$ si y solo si ${\displaystyle f^{-1}(V)}$es un vecindario de x para cada vecindario V de${\displaystyle f(x)}$en Y .

Como un conjunto abierto es un conjunto que es una vecindad de todos sus puntos, una función ${\displaystyle f:X\to Y}$es continua en cada punto de X si y solo si es una función continua.

Si X y Y son espacios métricos, es equivalente a considerar la base de entornos de bolas abiertas centradas en x y f ( x ) en lugar de todos los barrios. Esto devuelve lo anterior${\displaystyle \varepsilon -\delta }$definición de continuidad en el contexto de espacios métricos. En los espacios topológicos generales, no existe la noción de cercanía o distancia. Sin embargo, si el espacio objetivo es un espacio de Hausdorff , sigue siendo cierto que f es continua en a si y solo si el límite de f cuando x se acerca a a es f ( a ). En un punto aislado, cada función es continua.

Dado ${\displaystyle x\in X,}$ un mapa ${\displaystyle f:X\to Y}$ es continuo en ${\displaystyle x}$ si y solo si siempre ${\displaystyle {\mathcal {B}}}$ es un filtro en ${\displaystyle X}$que converge a${\displaystyle x}$ en ${\displaystyle X,}$ que se expresa por escrito ${\displaystyle {\mathcal {B}}\to x,}$ entonces necesariamente ${\displaystyle f({\mathcal {B}})\to f(x)}$ en ${\displaystyle Y.}$ Si ${\displaystyle {\mathcal {N}}(x)}$denota el filtro de vecindario en${\displaystyle x}$ luego ${\displaystyle f:X\to Y}$ es continuo en ${\displaystyle x}$ si y solo si ${\displaystyle f({\mathcal {N}}(x))\to f(x)}$ en ${\displaystyle Y.}$^[15] Además, esto sucede si y solo si el prefiltro ${\displaystyle f({\mathcal {N}}(x))}$es una base de filtro para el filtro de vecindad de${\displaystyle f(x)}$ en ${\displaystyle Y.}$^[15]

Definiciones alternativas

Existen varias definiciones equivalentes para una estructura topológica y, por lo tanto, hay varias formas equivalentes de definir una función continua.

Secuencias y redes

En varios contextos, la topología de un espacio se especifica convenientemente en términos de puntos límite . En muchos casos, esto se logra especificando cuándo un punto es el límite de una secuencia , pero para algunos espacios que son demasiado grandes en algún sentido, se especifica también cuándo un punto es el límite de conjuntos más generales de puntos indexados por una secuencia dirigida. conjunto , conocido como redes . Una función es (Heine-) continua sólo si lleva límites de secuencias a límites de secuencias. En el primer caso, la preservación de los límites también es suficiente; en el segundo, una función puede preservar todos los límites de las secuencias y aun así dejar de ser continua, y la preservación de las redes es una condición necesaria y suficiente.

En detalle, una función ${\displaystyle f:X\to Y}$es secuencialmente continuo si siempre que una secuencia${\displaystyle \left(x_{n}\right)}$en X converge a un límite x , la secuencia${\displaystyle \left(f(\left(x_{n}\right)\right)}$converge af ( x ). Por tanto, las funciones secuencialmente continuas "conservan los límites secuenciales". Cada función continua es secuencialmente continua. Si X es un primer espacio contable y la elección contable se cumple, entonces también se cumple lo contrario: cualquier función que preserve los límites secuenciales es continua. En particular, si X es un espacio métrico, la continuidad secuencial y la continuidad son equivalentes. Para los espacios que no se cuentan por primera vez, la continuidad secuencial puede ser estrictamente más débil que la continuidad. (Los espacios para los que las dos propiedades son equivalentes se denominan espacios secuenciales.) Esto motiva la consideración de redes en lugar de secuencias en espacios topológicos generales. Las funciones continuas conservan los límites de las redes y, de hecho, esta propiedad caracteriza a las funciones continuas.

Por ejemplo, considere el caso de funciones con valores reales de una variable real: ^[16]

Teorema  -  Una función${\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} }$ es continuo en ${\displaystyle x_{0}}$si y solo si es secuencialmente continuo en ese punto.

Prueba

Proof. Assume that ${\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} }$ is continuous at ${\displaystyle x_{0}}$ (in the sense of ϵ − δ {\displaystyle \epsilon -\delta } continuity). Let ${\displaystyle \left(x_{n}\right)_{n\geq 1}}$ be a sequence converging at ${\displaystyle x_{0}}$ (such a sequence always exists, e.g. ${\displaystyle x_{n}=x,\forall n}$); since ${\displaystyle f}$ is continuous at ${\displaystyle x_{0}}$ $${\displaystyle \forall \epsilon >0\,\exists \delta _{\epsilon }>0:0<|x-x_{0}|<\delta _{\epsilon }\implies |f(x)-f(x_{0})|<\epsilon .\quad (*)}$$ For any such ${\displaystyle \delta _{\epsilon }}$ we can find a natural number ${\displaystyle \nu _{\epsilon }>0}$ such that ${\displaystyle \forall n>\nu _{\epsilon }}$ $${\displaystyle |x_{n}-x_{0}|<\delta _{\epsilon },}$$ since ${\displaystyle \left(x_{n}\right)}$ converges at ${\displaystyle x_{0}}$; combining this with ${\displaystyle (*)}$ we obtain $${\displaystyle \forall \epsilon >0\,\exists \nu _{\epsilon }>0:\forall n>\nu _{\epsilon }\quad |f(x_{n})-f(x_{0})|<\epsilon .}$$ Assume on the contrary that ${\displaystyle f}$ is sequentially continuous and proceed by contradiction: suppose ${\displaystyle f}$ is not continuous at ${\displaystyle x_{0}}$ $${\displaystyle \exists \epsilon >0:\forall \delta _{\epsilon }>0,\,\exists x_{\delta _{\epsilon }}:0<|x_{\delta _{\epsilon }}-x_{0}|<\delta _{\epsilon }\implies |f(x_{\delta _{\epsilon }})-f(x_{0})|>\epsilon }$$ then we can take ${\displaystyle \delta _{\epsilon }=1/n,\,\forall n>0}$ and call the corresponding point ${\displaystyle x_{\delta _{\epsilon }}=:x_{n}}$: in this way we have defined a sequence ${\displaystyle (x_{n})_{n\geq 1}}$ such that $${\displaystyle \forall n>0\quad |x_{n}-x_{0}|<{\frac {1}{n}},\quad |f(x_{n})-f(x_{0})|>\epsilon }$$ by construction ${\displaystyle x_{n}\to x_{0}}$ but ${\displaystyle f(x_{n})\not \to f(x_{0})}$, which contradicts the hypothesis of sequentially continuity. ∎

Definiciones de operador de cierre y operador interior

En términos del operador interior , una función${\displaystyle f:X\to Y}$ entre espacios topológicos es continuo si y solo si para cada subconjunto ${\displaystyle B\subseteq Y,}$

$${\displaystyle f^{-1}\left(\operatorname {int} _{Y}B\right)~\subseteq ~\operatorname {int} _{X}\left(f^{-1}(B)\right).}$$

En términos del operador de cierre ,${\displaystyle f:X\to Y}$ es continuo si y solo si para cada subconjunto ${\displaystyle A\subseteq X,}$

$${\displaystyle f\left(\operatorname {cl} _{X}A\right)~\subseteq ~\operatorname {cl} _{Y}(f(A)).}$$

Es decir, dado cualquier elemento ${\displaystyle x\in X}$ que pertenece al cierre de un subconjunto ${\displaystyle A\subseteq X,}$ ${\displaystyle f(x)}$ pertenece necesariamente al cierre de ${\displaystyle f(A)}$ en ${\displaystyle Y.}$ Si declaramos que un punto ${\displaystyle x}$está cerca de un subconjunto${\displaystyle A\subseteq X}$ Si ${\displaystyle x\in \operatorname {cl} _{X}A,}$entonces esta terminología permite una descripción sencilla en inglés de la continuidad:${\displaystyle f}$ es continuo si y solo si para cada subconjunto ${\displaystyle A\subseteq X,}$ ${\displaystyle f}$ mapea puntos que están cerca de ${\displaystyle A}$ a puntos cercanos a ${\displaystyle f(A).}$ Similar, ${\displaystyle f}$ es continuo en un punto dado fijo ${\displaystyle x\in X}$ si y solo si siempre ${\displaystyle x}$ está cerca de un subconjunto ${\displaystyle A\subseteq X,}$ luego ${\displaystyle f(x)}$ esta cerca de ${\displaystyle f(A).}$

En lugar de especificar espacios topolgicos por sus subconjuntos abiertos , cualquier topologa en${\displaystyle X}$alternativamente, puede ser determinado por un operador de cierre o por un operador interior . Específicamente, el mapa que envía un subconjunto${\displaystyle A}$ de un espacio topológico ${\displaystyle X}$a su cierre topológico ${\displaystyle \operatorname {cl} _{X}A}$satisface los axiomas de cierre de Kuratowski y, a la inversa, para cualquier operador de cierre ${\displaystyle A\mapsto \operatorname {cl} A}$ existe una topología única ${\displaystyle \tau }$ en ${\displaystyle X}$ (específicamente, ${\displaystyle \tau :=\{X\setminus \operatorname {cl} A:A\subseteq X\}}$) tal que para cada subconjunto ${\displaystyle A\subseteq X,}$ ${\displaystyle \operatorname {cl} A}$ es igual al cierre topológico ${\displaystyle \operatorname {cl} _{X}A}$ de ${\displaystyle A}$ en ${\displaystyle (X,\tau ).}$ Si los conjuntos ${\displaystyle X}$ y ${\displaystyle Y}$ están asociados cada uno con los operadores de cierre (ambos denotados por ${\displaystyle \operatorname {cl} }$) luego un mapa ${\displaystyle f:X\to Y}$ es continuo si y solo si ${\displaystyle f\left(\operatorname {cl} A\right)\subseteq \operatorname {cl} (f(A))}$ para cada subconjunto ${\displaystyle A\subseteq X.}$

Del mismo modo, el mapa que envía un subconjunto ${\displaystyle A}$ de ${\displaystyle X}$a su interior topológico ${\displaystyle \operatorname {int} _{X}A}$define un operador interior y, a la inversa, cualquier operador interior${\displaystyle A\mapsto \operatorname {int} A}$ induce una topología única ${\displaystyle \tau }$ en ${\displaystyle X}$ (específicamente, ${\displaystyle \tau :=\{\operatorname {int} A:A\subseteq X\}}$) tal que para cada ${\displaystyle A\subseteq X,}$ ${\displaystyle \operatorname {int} A}$ es igual al interior topológico ${\displaystyle \operatorname {int} _{X}A}$ de ${\displaystyle A}$ en ${\displaystyle (X,\tau ).}$ Si los conjuntos ${\displaystyle X}$ y ${\displaystyle Y}$ están cada uno asociado con operadores interiores (ambos denotados por ${\displaystyle \operatorname {int} }$) luego un mapa ${\displaystyle f:X\to Y}$ es continuo si y solo si ${\displaystyle f^{-1}\left(\operatorname {int} B\right)\subseteq \operatorname {int} \left(f^{-1}(B)\right)}$ para cada subconjunto ${\displaystyle B\subseteq Y.}$^[17]

Filtros y prefiltros

La continuidad también se puede caracterizar en términos de filtros . Una función${\displaystyle f:X\to Y}$es continuo si y solo si siempre que un filtro ${\displaystyle {\mathcal {B}}}$ en ${\displaystyle X}$ converge en${\displaystyle X}$ a un punto ${\displaystyle x\in X,}$luego el prefiltro ${\displaystyle f({\mathcal {B}})}$ converge en ${\displaystyle Y}$ para ${\displaystyle f(x).}$Esta caracterización sigue siendo cierta si la palabra "filtro" se reemplaza por "prefiltro". ^[15]

Propiedades

Si ${\displaystyle f:X\to Y}$ y ${\displaystyle g:Y\to Z}$ son continuos, entonces también lo es la composición ${\displaystyle g\circ f:X\to Z.}$ Si ${\displaystyle f:X\to Y}$ es continuo y

• X es compacto , entonces f ( X ) es compacto.
• X está conectado , luego f ( X ) está conectado.
• X está conectado con la ruta , luego f ( X ) está conectado con la ruta.
• X es Lindelöf , luego f ( X ) es Lindelöf.
• X es separable , entonces f ( X ) es separable.

Las topologías posibles en un conjunto fijo X están parcialmente ordenadas : una topología${\displaystyle \tau _{1}}$se dice que es más tosco que otra topología${\displaystyle \tau _{2}}$ (notación: ${\displaystyle \tau _{1}\subseteq \tau _{2}}$) si cada subconjunto abierto con respecto a ${\displaystyle \tau _{1}}$ también está abierto con respecto a ${\displaystyle \tau _{2}.}$Luego, el mapa de identidad

$${\displaystyle \operatorname {id} _{X}:\left(X,\tau _{2}\right)\to \left(X,\tau _{1}\right)}$$

es continuo si y solo si ${\displaystyle \tau _{1}\subseteq \tau _{2}}$(ver también comparación de topologías ). De manera más general, una función continua

$${\displaystyle \left(X,\tau _{X}\right)\to \left(Y,\tau _{Y}\right)}$$

permanece continuo si la topología ${\displaystyle \tau _{Y}}$se reemplaza por una topología más tosca y / o${\displaystyle \tau _{X}}$se reemplaza por una topología más fina .

Homeomorfismos

Simétrico al concepto de mapa continuo es un mapa abierto , para el cual se abren imágenes de conjuntos abiertos. De hecho, si un mapa abierto f tiene una función inversa , esa inversa es continua, y si un mapa continuo g tiene una inversa, esa inversa es abierta. Dada una función biyectiva f entre dos espacios topológicos, la función inversa${\displaystyle f^{-1}}$no necesita ser continuo. Una función continua biyectiva con función inversa continua se llama homeomorfismo .

Si una biyección continua tiene como dominio un espacio compacto y su codominio es Hausdorff , entonces es un homeomorfismo.

Definición de topologías mediante funciones continuas

Dada una función

$${\displaystyle f:X\to S,}$$

donde X es un espacio topológico y S es un conjunto (sin una topología especificada), la topología final en S se define dejando que los conjuntos abiertos de S sean aquellos subconjuntos A de S para los cuales${\displaystyle f^{-1}(A)}$está abierto en X . Si S tiene una topología existente, f es continua con respecto a esta topología si y sólo si la topología existente es más gruesa que la topología final sobre S . Por lo tanto, la topología final se puede caracterizar como la topología más fina en S que hace que f sea continua. Si f es sobreyectiva , esta topología se identifica canónicamente con la topología del cociente bajo la relación de equivalencia definida por f .

Dualmente, para una función f desde un conjunto S a un espacio topológico X , la topología inicial en S se define designando como un conjunto abierto cada subconjunto A de S tal que${\displaystyle A=f^{-1}(U)}$por algún subconjunto abierto U de X . Si S tiene una topología existente, f es continua con respecto a esta topología si y sólo si la topología existente es más fina que la topología inicial en S . Por lo tanto, la topología inicial se puede caracterizar como la topología más burda en S que hace que f sea continua. Si f es inyectiva, esta topología se identifica canónicamente con la topología del subespacio de S , visto como un subconjunto de X .

Una topología en un conjunto S está determinada únicamente por la clase de todas las funciones continuas${\displaystyle S\to X}$en todos los espacios topológicos X . Dualmente , se puede aplicar una idea similar a los mapas.${\displaystyle X\to S.}$

Nociones relacionadas

Si ${\displaystyle f:S\to Y}$ es una función continua de algún subconjunto ${\displaystyle S}$ de un espacio topológico ${\displaystyle X}$ luego un extensión continua de${\displaystyle f}$ para ${\displaystyle X}$ es cualquier función continua ${\displaystyle F:X\to Y}$ tal que ${\displaystyle F(s)=f(s)}$ para cada ${\displaystyle s\in S,}$ que es una condición que a menudo se escribe como ${\displaystyle f=F{\big \vert }_{S}.}$ En palabras, es cualquier función continua. ${\displaystyle F:X\to Y}$que se restringe a${\displaystyle f}$ en ${\displaystyle S.}$Esta noción se utiliza, por ejemplo, en el teorema de extensión de Tietze y en el teorema de Hahn-Banach . Eran${\displaystyle f:S\to Y}$si no es continuo, no es posible que tenga una extensión continua. Si${\displaystyle Y}$es un espacio de Hausdorff y${\displaystyle S}$es un subconjunto denso de${\displaystyle X}$ luego una extensión continua de ${\displaystyle f:S\to Y}$ para ${\displaystyle X,}$ si existe, será único.

Varios otros dominios matemáticos utilizan el concepto de continuidad en significados diferentes pero relacionados. Por ejemplo, en la teoría del orden , una función de conservación del orden${\displaystyle f:X\to Y}$entre tipos particulares de conjuntos X e Y parcialmente ordenados es continua si para cada subconjunto dirigido A de X , tenemos${\displaystyle \sup f(A)=f(\sup A).}$ Aquí ${\displaystyle \,\sup \,}$es el superior con respecto a los ordenamientos en X e Y , respectivamente. Esta noción de continuidad es la misma que la de continuidad topológica cuando los conjuntos parcialmente ordenados reciben la topología de Scott . ^{[18] [19]}

En la teoría de categorías , un funtor

$${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$$

entre dos categorías se llama continuo , si conmuta con pequeños límites . Es decir,

$${\displaystyle \varprojlim _{i\in I}F(C_{i})\cong F\left(\varprojlim _{i\in I}C_{i}\right)}$$

para cualquier diagrama pequeño (es decir, indexado por un conjunto I , en contraposición a una clase ) de objetos en${\displaystyle {\mathcal {C}}}$.

Un espacio de continuidad es una generalización de espacios métricos y posets, ^{[20] [21]} que usa el concepto de quantales , y que puede usarse para unificar las nociones de espacios y dominios métricos . ^[22]

Ver también

• Continuidad absoluta
• Clasificación de discontinuidades
• Función gruesa
• Función continua (teoría de conjuntos)
• Proceso estocástico continuo
• Continuidad Dini
• Equicontinuidad
• Función normal
• Mapas abiertos y cerrados
• Por partes
• Función simétricamente continua

• Función de preservación de la dirección : análogo de una función continua en espacios discretos.

Referencias

1. Bolzano, Bernard (1817), Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey Werthen, die ein entgegengesetztes Resultat gewaehren, wenigstens eine reele Wurzel der Gleichung liege , Praga: Haase
2. Dugac, Pierre (1973), "Eléments d'Analyse de Karl Weierstrass", Archivo de Historia de las Ciencias Exactas , 10 : 41-176, doi : 10.1007 / bf00343406 , S2CID 122843140 
3. Goursat, E. (1904), Un curso de análisis matemático , Boston: Ginn, p. 2
4. Jordan, MC (1893), Cours d'analyse de l'École polytechnique , 1 (2.a ed.), París: Gauthier-Villars, p. 46
5. Harper, JF (2016), "Definición de la continuidad de las funciones reales de las variables reales", BSHM Bulletin: Journal of the British Society for the History of Mathematics , 31 (3): 1-16, doi : 10.1080 / 17498430.2015.1116053 , S2CID 123997123 
6. Rusnock, P .; Kerr-Lawson, A. (2005), "Bolzano y continuidad uniforme", Historia Mathematica , 32 (3): 303–311, doi : 10.1016 / j.hm.2004.11.003
7. Speck, Jared (2014). "Continuidad y discontinuidad" (PDF) . MIT Math . pag. 3 . Consultado el 2 de septiembre de 2016 . Ejemplo 5. La función ${\displaystyle 1/x}$ es continuo en ${\displaystyle (0,\infty )}$ y en ${\displaystyle (-\infty ,0),}$ es decir, para ${\displaystyle x>0}$ y para ${\displaystyle x<0,}$en otras palabras, en cada punto de su dominio. Sin embargo, no es una función continua ya que su dominio no es un intervalo. Tiene un solo punto de discontinuidad, a saber${\displaystyle x=0,}$ y tiene una discontinuidad infinita allí.
8. Lang, Serge (1997), Análisis de pregrado , Textos de pregrado en matemáticas (2a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-94841-6, sección II.4
9. Introducción al análisis real , actualizado en abril de 2010, William F. Trench, Teorema 3.5.2, p. 172
10. Introducción al análisis real , actualizado en abril de 2010, William F. Trench, 3.5 "Una mirada más avanzada a la existencia de la integral de Riemann adecuada", págs. 171-177
11. "Cálculo elemental" . wisc.edu .
12. Brown, James Ward (2009), Variables complejas y aplicaciones (8ª ed.), McGraw Hill, p. 54, ISBN 978-0-07-305194-9
13. Gaal, Steven A. (2009), Topología de conjuntos de puntos , Nueva York: Publicaciones de Dover , ISBN 978-0-486-47222-5, sección IV.10
14. Searcóid, Mícheál Ó (2006), espacios métricos , serie de matemáticas de pregrado de Springer, Berlín, Nueva York: Springer-Verlag , ISBN 978-1-84628-369-7, sección 9.4
15. Dugundji , 1966 , págs. 211-221.
16. Shurman, Jerry (2016). Cálculo y análisis en el espacio euclidiano (edición ilustrada). Saltador. págs. 271–272. ISBN 978-3-319-49314-5.
17. "topología general - Continuidad e interior" . Intercambio de pila de matemáticas .
18. Goubault-Larrecq, Jean (2013). Topología y teoría de dominios que no son de Hausdorff: temas seleccionados en topología de conjuntos de puntos . Prensa de la Universidad de Cambridge . ISBN 978-1107034136.
19. Gierz, G .; Hofmann, KH; Keimel, K .; Lawson, JD; Mislove, MW; Scott, DS (2003). Celosías y dominios continuos . Enciclopedia de Matemáticas y sus Aplicaciones. 93 . Prensa de la Universidad de Cambridge. ISBN 0521803381.
20. Flagg, RC (1997). "Quantales y espacios de continuidad". Álgebra Universalis . 37 (3): 257–276. CiteSeerX 10.1.1.48.851 . doi : 10.1007 / s000120050018 . S2CID 17603865 .  
21. Kopperman, R. (1988). "Todas las topologías provienen de métricas generalizadas". American Mathematical Monthly . 95 (2): 89–97. doi : 10.2307 / 2323060 . JSTOR 2323060 . 
22. Flagg, B .; Kopperman, R. (1997). "Espacios de continuidad: conciliación de dominios y espacios métricos" . Informática Teórica . 177 (1): 111-138. doi : 10.1016 / S0304-3975 (97) 00236-3 .

Bibliografía

• Dugundji, James (1966). Topología . Boston: Allyn y Bacon. ISBN 978-0-697-06889-7. OCLC  395340485 .
• "Función continua" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]